Have you ever wondered why we sometimes express binary numbers in hexadecimal format? Which is easier to remember: “1010 0101” or “A5”? If you find “A5” more convenient, you’re not alone. This is why we use hexadecimal to represent binary numbers.
Hexadecimal and Its Uses
You are viewing: Converting Binary to Hexadecimal: A Beginner’s Guide
Hexadecimal is a base 16 number system, which means it utilizes 16 numbers. It is commonly used in computing for various purposes, including representing colors, MAC addresses in networking, and memory addresses.
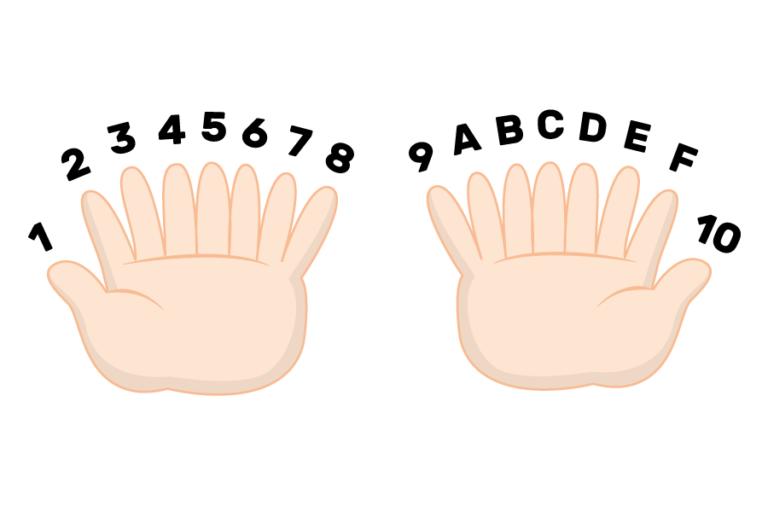
To give you an idea of how hexadecimal works, imagine a creature with 16 fingers counting using hexadecimal. Their counting sequence would be: 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10.
Conversion and Representation
Read more : Which Oil Is Best For Breast Massage During Pregnancy
In computing, hexadecimal is preferred because it can represent a byte of data with just two characters, compared to eight characters in binary. Each hexadecimal character represents half a byte, also known as a nibble. For example, hexadecimal 7D is equivalent to binary 0111 1101.
Converting binary to hexadecimal is also relatively simple. Let’s take the binary number 0001 1010 as an example. The first part, “0001,” represents the binary, denary, and hexadecimal number 1. The second part, “1010,” represents the denary number 10, which is equivalent to the hexadecimal “A.” Therefore, binary 0001 1010 is equal to hexadecimal 1A.
Converting Hexadecimal to Denary
Converting hexadecimal to denary can be done through binary. For instance, the hexadecimal number A9 is equivalent to binary 1010 1001. By using a conversion table, we can calculate the denary value of A9 as follows:
128 64 32 16 8 4 2 1
1 0 1 0 1 0 0 1Adding up the values where there is a “1,” we get: 128 + 32 + 8 + 1 = 169.
Alternatively, we can convert hexadecimal directly to denary by considering the place values. Just like in denary, hexadecimal uses a base value of 16. For example, converting hexadecimal A9 to denary:
16 (16¹) 1 (16⁰)
A 9Read more : Which Factor Does The Supreme Court Generally Consider
Referring to the conversion table, we know that A represents denary 10 and 9 represents denary 9. Hence, hexadecimal A9 equals (10 × 16) + (9 × 1) = 169 in denary.
Converting Denary to Hexadecimal
To convert denary to hexadecimal, we need to determine how many times 16 fits into the denary number. Let’s convert denary 200 to hexadecimal:
200 / 16 = 12, remainder 8Therefore, we have 12 lots of 16, with 8 units left over. In hexadecimal, denary 12 is represented as “C” and denary 8 as “8.” Thus, denary 200 equals (12 × 16) + (8 × 1) = C8 in hexadecimal.
Now it’s time to test your understanding! Try converting the following hexadecimal numbers into denary: 45, 2D, and E9. Good luck!
Source: https://t-tees.com
Category: WHICH
