Removable discontinuity is a subtopic of the topic continuity (or continuous functions). A function that is not continuous is said to have a discontinuity. The graphs of such functions cannot be drawn without lifting a pencil. There are mainly two types of discontinuities: removable discontinuity and nonremovable discontinuity.
Let us learn more about removable discontinuity and why it is called so along with examples.
You are viewing: Which Of The Functions Graphed Below Has A Removable Discontinuity
1. What is Removable Discontinuity? 2. Mathematical Definition of Removable Discontinuity 3. How to Remove the Removable Discontinuity? 4. Non Removable Discontinuity 5. Difference Between Non Removable and Removable Discontinuities 6. FAQs on Removable Discontinuity
The removable discontinuity is a type of discontinuity of functions that occurs at a point where the graph of a function has a hole in it. This point does not fit into the graph and hence there is a hole (or removable discontinuity) at this point. Consider a function y = f(x) and assume that it has removable discontinuity at a point (a, f(a)). Then one of the following two things can happen in the graph of f(x):
- Either f(a) is defined but (a, f(a)) doesn’t lie on the curve of the function
- or f(a) is NOT defined at all
We can see both the cases in the graph below:

In the above figure, in both the graphs, it seems like the graph is entirely continuous except at the hole, and so redefining the function at that particular point (as f(1) = -1 in this case) makes the function continuous. The discontinuity can be easily removed this way, and hence the name removable discontinuity.
Consider the first graph of the above figure. Clearly, the left-hand limit (lim ₓ → ₁₋ f(x)) and the right-hand limit (lim ₓ → ₁₊ f(x)) both are equal to -1. But f(1) = 1. i.e.,
- lim ₓ → ₁₋ f(x) = lim ₓ → ₁₊ f(x) (= -1) but
- The limits are NOT equal to f(1) (= 1)
In other words, lim ₓ → ₁ f(x) exists but is NOT equal to f(1) and we have seen that f(x) has a removable discontinuity at x = 1. Hence, we can define the removable discontinuity mathematically in one of the following ways:
- A function f(x) is said to have a removable discontinuity at x = a if and only if limₓ → ₐ₋ f(x) = limₓ → ₐ₊ f(x) ≠ f(a). [OR]
- A function f(x) is said to have a removable discontinuity at x = a if and only if limₓ → ₐ f(x) ≠ f(a).
Let us prove the removable discontinuity in each of the graphs in the above figure.
Read more : A Unicellular Protist Is Part Of Which Domain
The given function is f(x) = (x3 – 3×2 + 2x) / (x – 1). We will compute its limit at x = 1.
lim ₓ → ₁ f(x) = lim ₓ → ₁ (x3 – 3×2 + 2x) / (x – 1) = lim ₓ → ₁ [ x (x2 – 3x + 2) ] / (x – 1) = lim ₓ → ₁ [ x (x – 1) (x – 2) ] / (x – 1) = lim ₓ → ₁ [ x (x – 2) ] (as (x – 1) got canceled) = 1 (1 – 2) = -1
First Graph: f(1) = 1 and in this case, lim ₓ → ₁ f(x) ≠ f(1).
Second Graph: f(1) = (13 – 3(1)2 + 2(1)) / (1 – 1) = 0/0, which is an indeterminate form and hence f(1) is NOT defined. Here also, lim ₓ → ₁ f(x) ≠ f(1).
Thus, the removable discontinuities in both graphs are justified by the mathematical definition.
In each of the above examples, there was a removable discontinuity at x = 1 and it happened just because lim ₓ → ₁ f(x) ≠ f(1). This can be easily removed simply by defining f(1) as lim ₓ → ₁ f(x). In the above example, if we set the function as follows, the function will be continuous at x = 1.
(f(x)=left{begin{array}{ll} frac{x^{3}-3 x^{2}+2 x}{x-1}, & text { if } x neq 1 -1, & text { if } x = 1 end{array}right.)
As we found earlier, lim ₓ → ₁ f(x) = -1 and by the above definition of function, f(1) = -1. Hence, lim ₓ → ₁ f(x) = f(1) in this case, and hence the function is continuous at x = 1.
Thus, here are the steps to remove the removable discontinuity of a function f(x) at x = a.
- Find limₓ → ₐ f(x) (call it as L).
- Define f(a) = L.
In contrary to the removable discontinuity, a function f(x) has non removable discontinuity at x = a if the limit limₓ → ₐ f(x) does not exist. There are two types of nonremovable discontinuities:
- Jump Discontinuity
- Infinite Discontinuity
Jump Discontinuity
Read more : Which Of These Common Substances Is A Homogeneous Mixture
If a function f(x) has a jump discontinuity at x = a, then the curve of the function jumps at x = a from one place to another place. This is because the left-hand limit (limₓ → ₐ₋ f(x)) and the right-hand limit (limₓ → ₐ₊ f(x)) exist but they are NOT equal. Since the limit itself doesn’t exist in jump discontinuity, we don’t need to worry about whether limit is equal to f(a). The jump discontinuity looks as follows:
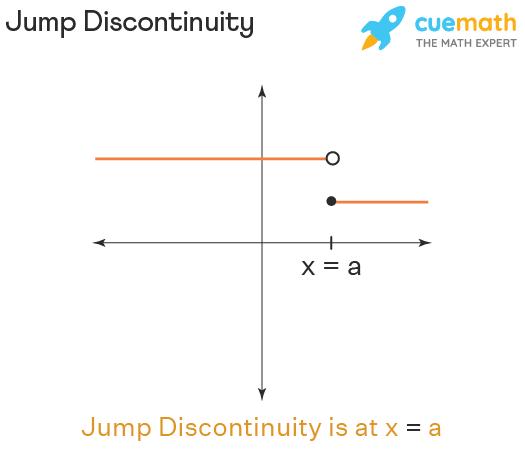
Hence, the jump discontinuity of a function f(x) at x = a is defined mathematically as follows:
- limₓ → ₐ₋ f(x) and limₓ → ₐ₊ f(x) exist and they are NOT equal [OR]
- limₓ → ₐ₋ f(x) ≠ limₓ → ₐ₊ f(x)
Infinite Discontinuity
If a function has an infinite discontinuity then one or both of the left-hand and right-hand limits is equal to ± ∞. For example, a function f(x) has infinite discontinuity when limₓ → ₐ₋ f(x) = ∞ and/or limₓ → ₐ₊ f(x) = -∞. The graph of a function having infinite discontinuity looks as follows:
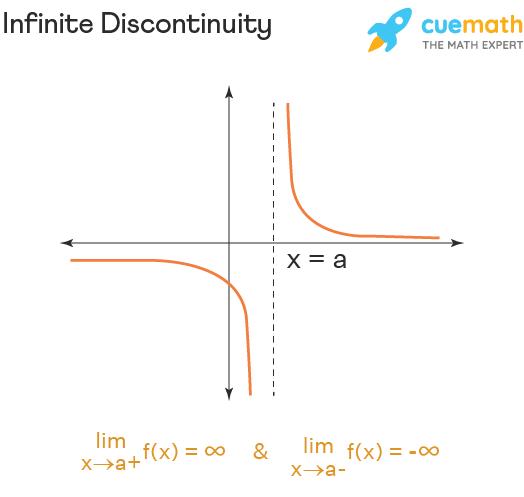
By the above graph, it is so obvious that an infinite discontinuity occurs at a vertical asymptote. The above graph has a vertical asymptote at x = a.
We now have a very clear idea of what is removable discontinuity and nonremovable discontinuity. The following table summarizes the differences between them. In each case, assume that a function f(x) is discontinuous at x = a.
Removable Discontinuity Non Removable Discontinuity 1. Limit exists at the point of discontinuity. 1. Limit does not exist at the point of discontinuity. 2. limₓ → ₐ f(x) ≠ f(a) 2. When limₓ → ₐ f(x) doesn’t exist, we don’t need to think about whether the limit equals f(a). 3. Graphically: This occurs when the graph is such that it is possible to make it continuous just by filling the gap of discontinuity. 3. Graphically: This occurs when the graph jumps or tends to ± ∞ at x = a. 4. Mathematically: This mostly occurs when (x – a) is a factor of both numerator and denominator (or in other words, there is a hole at x = a) 4. Mathematically: This mostly occurs when left and right-hand limits are not the same (or) when x = a is a vertical asymptote.
Important Notes on Removable Discontinuity:
- There are 3 types of discontinuities: (i) Removable discontinuity (ii) Jump discontinuity and (iii) Infinite discontinuity
- Removable discontinuity formula: limₓ → ₐ f(x) ≠ f(a)
- Jump discontinuity formula: limₓ → ₐ₋ f(x) ≠ limₓ → ₐ₊ f(x)
- Infinite discontinuity formula: limₓ → ₐ₋ f(x) and/or limₓ → ₐ₊ f(x) = ∞ or -∞
☛ Related Topics:
- Limits Calculator
- Calculus Calculator
- Derivatives
Source: https://t-tees.com
Category: WHICH
