Direct Variation Definition
Two quantities as said to follow a direct variation if both increase or decrease by the same factor. Thus, an increase in one quantity leads to an increase in the other while a decrease in one quantity leads to a decrease in the other. In other words, if the ratio of the first quantity to the second quantity is a constant term, then the quantities are said to be directly proportional to each other. This constant value is known as the coefficient or constant of proportionality.
Direct Variation Example
The following two quick examples are helpful for an easy understanding of this concept of direct variation.
You are viewing: Which Representation Has A Constant Of Variation Of -2.5
Example I: The formula for the circumference of a circle is given by C = 2πr or C = πd. Here, r is the radius and d is the diameter. This is an example of a direct variation. Thus, the circumference of a circle and its corresponding diameter are in direct variation with π being the constant of proportionality.
Example II: The quantity of Iron boxes made is directly proportional to the number of iron blocks. The number of iron blocks needed for 40 boxes is 160. How many iron blocks are needed for a box?
In the given problem, the number of iron blocks needed for 40 boxes is referred to as y = 160, and the number of boxes is referred to as x = 40. The number of iron blocks needed for a box is k. Here we use the direct variation formula of y = kx.
160 = k × 40 k = 160/40 k = 4
Thus 4 iron blocks are needed for a box.
Direct variation formula helps relate two quantities, having a mathematical relationship such that one of the variables is a constant multiple of the other. When two quantities are directly proportional to each other or are in direct variation they are represented using the symbol “(propto)”. Suppose there are two quantities x and y that are in direct variation then they are expressed as follows:
Read more : Which Us Marathon Provides The Most Money
y (propto) x
When the proportionality sign is removed then the direct variation formula is given as follows.
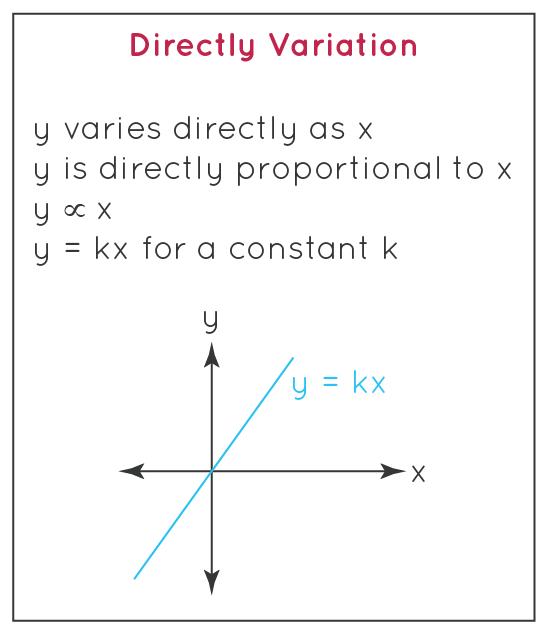
Direct Variation Formula: y = kx
Here k is the constant of proportionality. If x is not equal to zero then the value of the constant of proportionality can be given as k = y/x. Thus, the ratio of these two variables is always a constant number. Another way of expressing the direct variation equation is x = y / k. This means that x is directly proportional to y with the constant of proportionality equalling 1 / k.
The formula for the direction variation for a set of two quantities that are linearly dependent is as follows.

Let us understand the formula of direct variation with the help of a simple example. Example: Let us assume that y varies directly with x, and y = 30 when x = 6. What is the value of y when x = 100?
The given quantities are y1 = 30, x1 = 6, x2 = 100, y2 = ? Using direct variation formula we have the following expression.
y1 / x1 = y2 / x2 30/6 = y2 / 1005 = y2 / 100 y2 = 500
Read more : Which Icu Is The Hardest
Therefore the value of y when x = 100 is 500.
The graph of two quantities in a direct variation will result in a straight line. Thus, direct variation represents a linear equation in two variables. The linear equation is given by y = kx. The ratio of change (frac{Delta y}{Delta x}) is also equal to k. This change represents the slope of the line. The direct variation graph is given as follows:
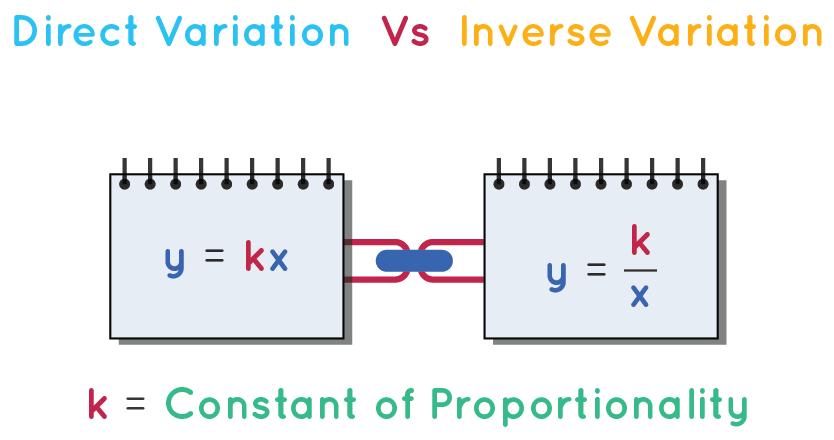
Inverse and direct variation are both types of proportionalities. The difference between inverse and direct variation is given in the table below:
Direct Variation Inverse Variation When one quantity increases (or decreases) with an increase (or decrease) in another quantity it is a direct variation. When one quantity increases with a decrease in another quantity or vice versa it results in an inverse variation. The ratio of the two quantities will always be constant (constant of proportionality). The product of the two quantities will always be a constant (constant of proportionality). It is expressed as y (propto) x y (propto) 1 / x The direct variation formula is y = kx The inverse variation formula is given by y = k / x The graph of a direct variation is a straight line. The graph of an inverse variation is a rectangular hyperbola.
Related Articles:
- Direct Proportion
- Ratio and Proportion
- Percent Proportion
Important Notes on Direct Variation
- A direct variation is a proportionality relationship in which two quantities follow a direct relationship. This implies that an increase (or decrease) in one quantity leads to a corresponding increase (or decrease) in another quantity.
- The direct variation equation is a linear equation in two variables and is given by y = kx where k is the constant proportionality.
- The direct variation graph in a coordinate plane is a straight line.
- The ratio of two quantities in a direct variation is a constant.
Source: https://t-tees.com
Category: WHICH
