A circle is defined as the locus of a moving point on a plane such that its distance from a fixed point on the plane remains constant or fixed. That fixed point is called the center of the circle. Let us learn more about the center of a circle in this article.
1. Center of Circle Definition 2. Center of Circle Formula 3. How to Find Center of Circle? 4. FAQs on Center of Circle
You are viewing: What Is The Center Of The Circle Shown Below
A circle is a 2D shape defined by its center and radius. We can draw any circle if we know the center of circle and its radius. A circle can have an infinite number of radii. The center of a circle is the midpoint where all the radii meet. It can also be defined as the midpoint of the diameter of the circle. Observe the figure given below where O is the center of circle and OP is the radius.
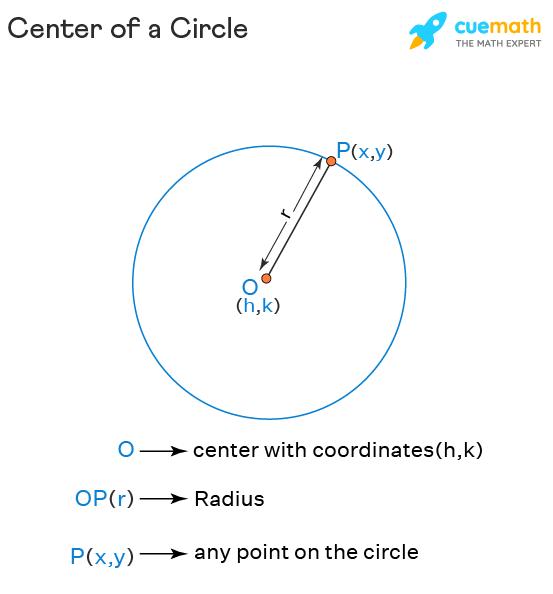
The center of circle formula is also known as the general equation of a circle. In a circle, if the coordinates of the center are (h,k), r is the radius, and (x,y) is any point on the circle, then the center of circle formula is given below:
(x – h)2 + (y – k)2 = r2
This is also known as the center of the circle equation. We will be using this formula in the following sections to find the center of a circle or the equation of the circle.
In order to find the center of the circle, we will use some simple steps. There are two cases that might come up when we could be asked to find the center of a circle:
- When a circle is given and we need to find its center.
- When an equation of a circle is given and we need to find the coordinates of its center.
When a Circle is Given
When a circle is given to us and we need to find its center point, then we can follow the steps listed below:
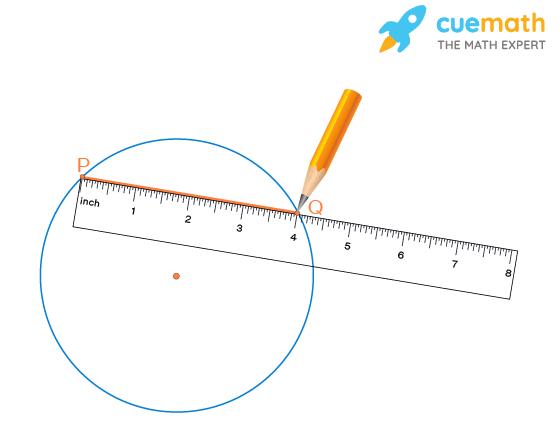
Step 1: Draw a chord PQ in a circle and carefully note its length (which is 4 inches in the figure below).
Read more : What Happens In Iron Flame
Step 2: Draw another chord MN parallel to PQ such that it should be of the same length as PQ.
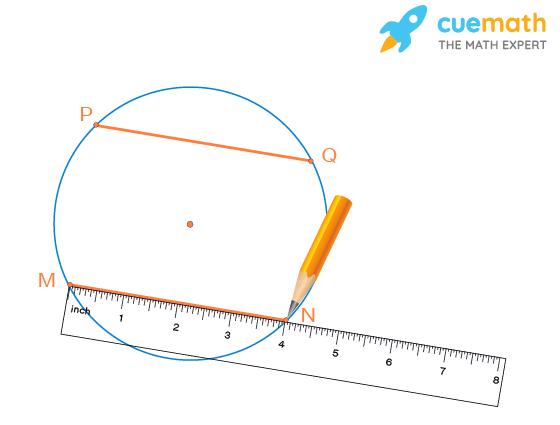
Step 3: Join the points P and N through a line segment using a ruler.
Step 4: Join points Q and M.
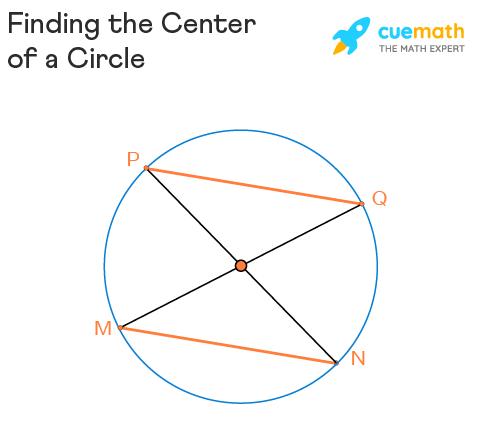
Step 5: The point of intersection of PN and QM is the center of the circle.
When Equation of the Circle is Given
If we know the equation of a circle, and we need to find its center, then we will use the following steps. Let us understand this with the help of an example.
Example: Let us find the coordinates of the center of a circle with equation x2 + y2 – 4x – 6y – 87 = 0
Solution: The steps to find the coordinates of the center of a circle are listed below:
- Step 1: Write the given equation in the form of the general equation of a circle: (x – h)2 + (y – k)2 = r2, by adding or subtracting numbers on both sides.
We can write the given equation as x2 – 4x + y2 – 6y = 87. Add 4 to both sides of the equation to get a perfect square of x-2. So, we will get, x2 – 4x + 4 + y2 – 6y = 87 + 4.
⇒ (x – 2)2 + y2 – 6y = 91
Add 9 to both sides to get a perfect square of y – 3
Read more : What Shampoos Are Good For Oily Hair
⇒ (x – 2)2 + y2 – 6y + 9 = 91 + 9
⇒ (x – 2)2 + (y – 3)2 = 100
⇒ (x – 2)2 + (y – 3)2 = 102
This looks like the general equation of circle.
- Step 2: Compare this equation with the general equation and identify the values of h, k, and r.
If we compare (x – 2)2 + (y – 3)2 = 102 with (x – h)2 + (y – k)2 = r2, we can identify that h = 2, k = 3, and r = 10. So, we have got the coordinates of the center of circle which are (h, k) = (2, 3).
How to Find the Center of Circle with Two Points?
If the endpoints of the diameter of the circle are given, then to find the coordinates of the center we use the mid-point formula, because the center is the mid-point of the diameter of the circle. The steps to find the center of a circle with two points are given below:
- Step 1: Assume that the coordinates of the center of the circle are (h, k).
- Step 2: Use the midpoint formula which says that if (h, k) are the coordinates of the midpoint of a segment with endpoints (x1, y1) and (x2, y2), then (h, k) = [(x1 + x2]/2, [y1 + y2]/2).
- Step 3: Simplify it and get the coordinates of the center of the circle.
Let us take an example of a circle in which the endpoints of a diameter are given as (-2, 4), and (6, 16). Then, the coordinates of its center are:
(h, k) = [(-2 + 6)/2, (4 + 16)/2]
(h, k) = (4/2, 20/2)
(h, k) = (2, 10)
Therefore, the coordinates of the center of a circle with the endpoints of diameter are (2, 10).
☛ Related Articles
Check these interesting articles related to the concept of center of circle in geometry.
- Circle Formulas
- Sector of a Circle
- Circumference of Circle
- Area of Circle
Source: https://t-tees.com
Category: WHAT
