Which Expression Illustrates The Associative Property Of Addition

What Is Associative Property in Math?

Associative property is defined as, when more than two numbers are added or multiplied, the result remains the same, irrespective of how they are grouped.

For instance,

You are viewing: Which Expression Illustrates The Associative Property Of Addition

2 × (7 × 6) = (2 × 7) × 6

2 + (7 + 6) = (2 + 7) + 6

Associative Property of Addition

Associative property for addition implies that regardless of how numbers are grouped, the final sum of the numbers will remain the same. This can be expressed as:

(x + y) + z = x + (y + z)

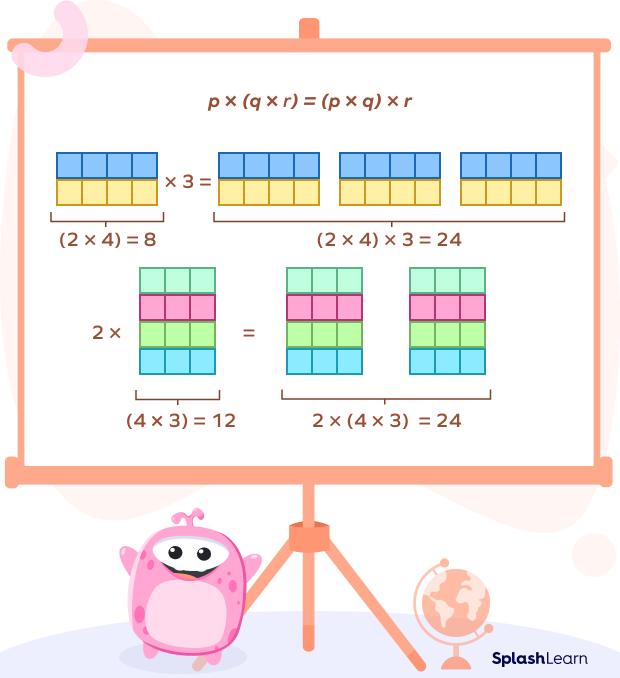
Associative Property of Multiplication

Associative property for multiplication implies that regardless of how numbers are grouped, the final product of the numbers will remain the same. This can be expressed as:

p × (q × r) = (p × q) × r

Difference between Associative Property and Commutative Property

Commutative Property

Commutative Property implies that when multiplication or addition is performed on two numbers, the result remains the same, irrespective of their arrangement.

Now, when you know about both the properties, you must have figured out that the only difference lies in the number of numbers involved in the operation.

Two numbers are involved in commutative property and more than two numbers are involved in associative property.

Is Associative Property Applicable to Division and Subtraction?

You must be wondering why these properties don’t apply to division and subtraction. Let’s take an example to answer this “Why?”.

In the case of subtraction:

12 – (6 – 2) = 12 – 4 = 8

(12 – 6) – 2 = 6 – 2 = 4

Read more : Which Bts Members Are Gay

This implies, 12 – (6 – 2) ≠ (12 – 6) – 2. So, the associative property is not applicable for subtraction.

In the case of division:

(24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3

24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12

This implies, (24 ÷ 4) ÷ 2 ≠ 24 ÷ (4 ÷ 2). So, the associative property is not applicable for the division.

Fun Fact!

The associative property gets its name from the word “associate”, and it refers to the grouping of numbers.

Solved Examples On Associative Property

Example 1: If (30 × 20) × 15 = 9000, then use associative property to find (15 × 30) × 20.

Solution: According to the associative property of multiplication, (30 × 20) × 15 = (15 × 30) × 20.

Given that (30 × 20) × 15 = 9000,

(15 × 30) × 20 = 9000.

Example 2: Check whether the associative property of addition is implied in the following equations.

1. 20 + (60 + 5) = (20 + 60) + 5
2. 30 + (40 + 20) = (30 + 10) + 50

Solution:

1. According to the associative property of addition, 20 + (60 + 5) = (20 + 60) + 5. Let’s check further.

LHS: 20 + (60 + 5)

20 +(65)

85

Read more : Which Sound Of Music Character Are You

RHS: (20 + 60) + 5

(80) + 5

85

LHS = RHS. Thus, the associative property of addition is implied in this equation.

1. According to the associative property of addition, 30 + (40 + 20) = (30 + 10) + 50. Let’s check further,

LHS: 30 + (40 + 20)

30 + (60)

90

RHS: (30 + 10) + 50

(40) + 50

90

LHS ≠ RHS. Thus, the associative property of addition is not implied in this equation.

Example 3: According to the associative property, fill in the missing number.

(5 + 10) + 4 = (5 + 4) + __ = 14

Solution: According to the associative property, when more than two numbers are added, the result remains the same irrespective of how they are grouped. Hence, (5 + 10) + 4 = (5 + 4) + 10 = 14

Practice Problems On Associative Property

Frequently Asked Questions On Associative Property

Source: https://t-tees.com
Category: WHICH