A compound inequality is a combination of two inequalities that are combined by either using “and” or “or”. The process of solving each of the inequalities in the compound inequalities is as same as that of a normal inequality but just while combining the solutions of both inequalities depends upon whether they are clubbed by using “and” or “or”.
Let us see the process of solving compound inequalities and also how to graph them on the number line.
You are viewing: Which Graph Represents The Compound Inequality
1. What is a Compound Inequality? 2. Compound Inequality Graph 3. Solving Compound Inequalities 4. FAQs on Compound Inequality
A compound inequality is an inequality that merges two inequalities either by using “and” or “or”. Sometimes “and” won’t be specifically mentioned but it is understood. For example, 1 < x < 3 is nothing but “x > 1 and x < 3”. On the other hand, a compound inequality with “or” is always specifically mentioned using “or”. The two types of compound inequalities are conjunction and disjunction and the following are the differences between them,
Conjunction Disjunction It is a compound inequality in which the inequalities are joined by using “AND”. It is a compound inequality in which the inequalities are joined by using “OR”. Example: -2 < x < 3 [or equivalently “x > -2 AND x < 3”] Example: x < -2 OR x > 3 They can be clubbed by using the “intersection” symbol (∩) between the intervals representing them. For example, x > -2 AND x < 3 can be written as (-2, ∞) ∩ (-∞, 3). They can be clubbed by using the “union” symbol (∪) between the intervals representing them. For example, x < -2 OR x > 3 can be written as (-∞, -2) ∪ (3, ∞). Since its an “AND”, the solution should contain the values that satisfy “BOTH” the inequalities. Since its an “OR”, the solution can contain the values that satisfy “Either or both” the inequalities.
We can graph the compound inequalities on the number line. Keep the following things in mind when graphing compound inequalities.
- First look for the number on the number line that the inequality has. For example, if we have x > 2, we need to see where 2 is on the number line.
- Put an open dot (to show that the value is NOT included) if the inequality is either “>” or “<“. Put a closed dot (to show that the value is included) if the inequality is either “≥” or “≤”. For example, if we have x > 2 then put an open dot at 2 as the inequality is a strict inequality and it doesn’t include “=”.
- For “>” or “≥” sign, draw an arrow to the right side of the number.
- For “<” or “≤” sign, draw an arrow to the left side of the number.
- For finding the final solution, just use the intersection or union depending on whether “AND” or “OR” is given respectively.
Example of Graphing Compound Inequality with AND
Graph the compound inequality x > 1 AND x ≤ 4.
We will graph each inequality on the number line as follows:
- x > 1: Since we don’t have “=” at 1 we get an open dot at 1. Also, we draw an arrow to the right of 1 as we have “>”.
- x ≤ 4: Since we have “=” at 4 we get a closed dot at 1. Also, we draw an arrow to the left of 4 as we have “≤”.
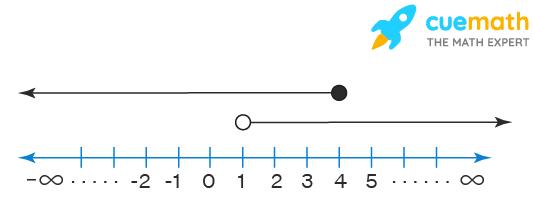
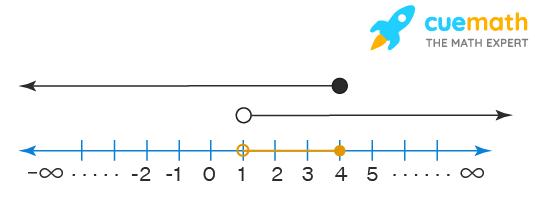
Finally, we look for the values on the number line that satisfy “BOTH” inequalities as the given compound inequality has “AND” in it. It is very clear from both arrows above that the region of intersection (common region) of both arrows is from 1 to 4 where 1 is not included and 4 is included. i.e., the solution of the given compound inequality is 1 < x ≤ 4 and is shown by a “orange” line on the number line below. In the interval notation, the solution can be written as (1, 4].
Example of Graphing Compound Inequality with OR
Graph the compound inequality x ≤ -1 OR x > 2.
We will graph each inequality on the number line as follows:
- x ≤ -1: Since we have “=” at 1 we get a closed dot at 1. Also, we draw an arrow to the left of 1 as we have “≤”.
- x > 2: Since we don’t have “=” at 2 we get an open dot at 2. Also, we draw an arrow to the right of 2 as we have “>”.
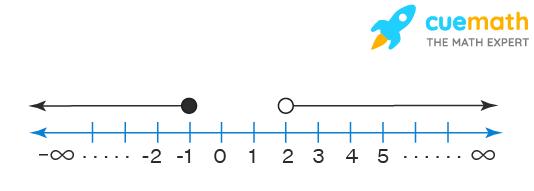
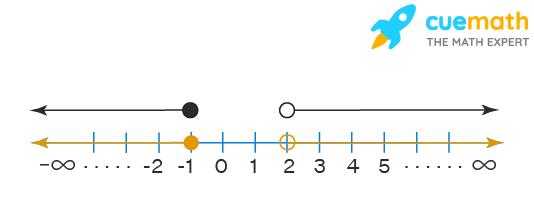
Since the given inequality has an “OR” in it, we just use “union” between them in the solution. Hence the solution is x ≤ -1 OR x > 2 itself. In the interval notation, the solution is, (-∞, -1] ∪ (2, ∞). The solution is shown with “orange” line on the number line below.
We know that a compound inequality is the merging of two simple inequalities. Hence, each of them can be solved in the same way as we solve a simple inequality (to know how to solve a simple inequality, click here) and then we club them according to what they gave (AND / OR) just like how it was explained in the previous section. Here is the step-by-step explanation of solving compound inequalities.
- Step 1: Identify two inequalities that are given in the given inequality.
- Step 2: Solve each of them just like how we solve a normal inequality. Note that the procedure of solving an inequality is as same as solving an equation but just reverse the sign of inequality when you are multiplying or dividing the inequality by a negative number.
- Step 3: Graph the solution of each inequality on the number line (as explained in the last section).
- Step 4: Take the “intersection” of the solutions if “AND” is given; and take the “union” of the solutions if “OR” is given.
If we are able to analyze the solution without graphing, then we can avoid Step 3. Graphing compound inequalities is not compulsory unless it is specifically mentioned to graph it. The above procedure is explained with examples (one of each of “AND” and “OR”) below.
Example of Solving Compound Inequality with AND
Solve the compound inequality -2 < 2x – 3 < 5.
We can solve it in two ways: one is without splitting into two; and the other is by splitting into two. Let us see both ways.
Method 1: The given compound inequality is -2 < 2x – 3 < 5.
Adding 3 on all the sides,
-2 + 3 < 2x – 3 + 3 < 5 + 3
1 < 2x < 8
Dividing all the sides by 2,
1/2 < 2x/2 < 8/2
1/2 < x < 4.
Hence, the direct solution is 1/2 < x < 4 (or) the interval (1/2, 4).
Method 2: Split the given inequality into two inequalities. Then we get
2x – 3 > -2 AND 2x – 3 < 5
Read more : Discover Which Character from The Office You Are
Adding 3 on both sides of each inequality,
2x > 1 AND 2x < 8
Dividing each inequality both sides by 2,
x > 1/2 AND x < 4
Again, merging them back,
1/2 < x < 4.
Hence, the solution is 1/2 < x < 4 (or) the interval (1/2, 4).
Example of Solving Compound Inequality with OR
Solve the compound inequality -3x – 1 > -7 OR -5x + 2 < -12.
Add 1 on both sides of the first inequality and subtract 2 from both sides of the second inequality.
-3x > -6 OR -5x < -14
Divide the first inequality on both sides by -3 and the second inequality by -5. Note that the sign of the inequality changes when we divide by a negative number.
x < 2 OR x > 2.8
Hence, the solution is (-∞, 2) U (2.8, ∞).
Important Notes on Compound Inequalities:
- A compound inequality involves more than one inequality merged with “AND” or “OR”.
- If two inequalities are merged with “AND”, then merge their solutions by taking the intersection.
- If two inequalities are merged with “OR”, then merge their solutions by taking the union.
- Graphing compound inequalities make the process of finding the union or intersection very easy.
- A compound inequality sometimes has “no solution” and sometimes it has “the set of all real numbers” as the solution.
☛ Related Topics:
- Linear Inequalities
- Quadratic Inequalities
- Absolute Value Inequalities
- Inequality Calculator
Source: https://t-tees.com
Category: WHICH
