In previous sections of this chapter, we were either given a function explicitly to graph or evaluate, or we were given a set of points that were guaranteed to lie on the curve. Then we used algebra to find the equation that fit the points exactly. In this section, we use a modeling technique called regression analysis to find a curve that models data collected from real-world observations. With regression analysis, we don’t expect all the points to lie perfectly on the curve. The idea is to find a model that best fits the data. Then we use the model to make predictions about future events.
Do not be confused by the word model. In mathematics, we often use the terms function, equation, and model interchangeably, even though they each have their own formal definition. The term model is typically used to indicate that the equation or function approximates a real-world situation.
You are viewing: Which Investment Data Is Best Modeled By An Exponential Function
We will concentrate on three types of regression models in this section: exponential, logarithmic, and logistic. Having already worked with each of these functions gives us an advantage. Knowing their formal definitions, the behavior of their graphs, and some of their real-world applications gives us the opportunity to deepen our understanding. As each regression model is presented, key features and definitions of its associated function are included for review. Take a moment to rethink each of these functions, reflect on the work we’ve done so far, and then explore the ways regression is used to model real-world phenomena.
Build an exponential model from data
As we’ve learned, there are a multitude of situations that can be modeled by exponential functions, such as investment growth, radioactive decay, atmospheric pressure changes, and temperatures of a cooling object. What do these phenomena have in common? For one thing, all the models either increase or decrease as time moves forward. But that’s not the whole story. It’s the way data increase or decrease that helps us determine whether it is best modeled by an exponential equation. Knowing the behavior of exponential functions in general allows us to recognize when to use exponential regression, so let’s review exponential growth and decay.
Recall that exponential functions have the form [latex]y=a{b}^{x}[/latex] or [latex]y={A}_{0}{e}^{kx}[/latex]. When performing regression analysis, we use the form most commonly used on graphing utilities, [latex]y=a{b}^{x}[/latex]. Take a moment to reflect on the characteristics we’ve already learned about the exponential function [latex]y=a{b}^{x}[/latex] (assume a > 0):
- b must be greater than zero and not equal to one.
- The initial value of the model is y = a.
- If b > 1, the function models exponential growth. As x increases, the outputs of the model increase slowly at first, but then increase more and more rapidly, without bound.
- If 0 < b < 1, the function models exponential decay. As x increases, the outputs for the model decrease rapidly at first and then level off to become asymptotic to the x-axis. In other words, the outputs never become equal to or less than zero.
Read more : Which Side Is Hot Water Under Sink
As part of the results, your calculator will display a number known as the correlation coefficient, labeled by the variable r, or [latex]{r}^{2}[/latex]. (You may have to change the calculator’s settings for these to be shown.) The values are an indication of the “goodness of fit” of the regression equation to the data. We more commonly use the value of [latex]{r}^{2}[/latex] instead of r, but the closer either value is to 1, the better the regression equation approximates the data.
Build a logarithmic model from data
Just as with exponential functions, there are many real-world applications for logarithmic functions: intensity of sound, pH levels of solutions, yields of chemical reactions, production of goods, and growth of infants. As with exponential models, data modeled by logarithmic functions are either always increasing or always decreasing as time moves forward. Again, it is the way they increase or decrease that helps us determine whether a logarithmic model is best.
Recall that logarithmic functions increase or decrease rapidly at first, but then steadily slow as time moves on. By reflecting on the characteristics we’ve already learned about this function, we can better analyze real world situations that reflect this type of growth or decay. When performing logarithmic regression analysis, we use the form of the logarithmic function most commonly used on graphing utilities, [latex]y=a+bmathrm{ln}left(xright)[/latex]. For this function
- All input values, x, must be greater than zero.
- The point (1, a) is on the graph of the model.
- If b > 0, the model is increasing. Growth increases rapidly at first and then steadily slows over time.
- If b < 0, the model is decreasing. Decay occurs rapidly at first and then steadily slows over time.
Build a logistic model from data
Like exponential and logarithmic growth, logistic growth increases over time. One of the most notable differences with logistic growth models is that, at a certain point, growth steadily slows and the function approaches an upper bound, or limiting value. Because of this, logistic regression is best for modeling phenomena where there are limits in expansion, such as availability of living space or nutrients.
It is worth pointing out that logistic functions actually model resource-limited exponential growth. There are many examples of this type of growth in real-world situations, including population growth and spread of disease, rumors, and even stains in fabric. When performing logistic regression analysis, we use the form most commonly used on graphing utilities:
Read more : Which Type Of Rocket Engine Is Used To Maneuver Bitlife
Recall that:
- [latex]frac{c}{1+a}[/latex] is the initial value of the model.
- when b > 0, the model increases rapidly at first until it reaches its point of maximum growth rate, [latex]left(frac{mathrm{ln}left(aright)}{b},frac{c}{2}right)[/latex]. At that point, growth steadily slows and the function becomes asymptotic to the upper bound y = c.
- c is the limiting value, sometimes called the carrying capacity, of the model.
Key Concepts
- Exponential regression is used to model situations where growth begins slowly and then accelerates rapidly without bound, or where decay begins rapidly and then slows down to get closer and closer to zero.
- We use the command “ExpReg” on a graphing utility to fit function of the form [latex]y=a{b}^{x}[/latex] to a set of data points.
- Logarithmic regression is used to model situations where growth or decay accelerates rapidly at first and then slows over time.
- We use the command “LnReg” on a graphing utility to fit a function of the form [latex]y=a+bmathrm{ln}left(xright)[/latex] to a set of data points.
- Logistic regression is used to model situations where growth accelerates rapidly at first and then steadily slows as the function approaches an upper limit.
- We use the command “Logistic” on a graphing utility to fit a function of the form [latex]y=frac{c}{1+a{e}^{-bx}}[/latex] to a set of data points.
Section Exercises
1. What situations are best modeled by a logistic equation? Give an example, and state a case for why the example is a good fit. 2. What is a carrying capacity? What kind of model has a carrying capacity built into its formula? Why does this make sense? 3. What is regression analysis? Describe the process of performing regression analysis on a graphing utility. 4. What might a scatterplot of data points look like if it were best described by a logarithmic model? 5. What does the y-intercept on the graph of a logistic equation correspond to for a population modeled by that equation? For the following exercises, match the given function of best fit with the appropriate scatterplot. Answer using the letter beneath the matching graph.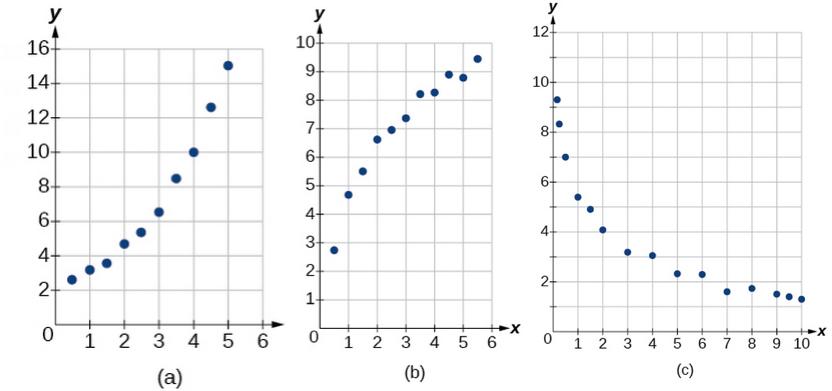 
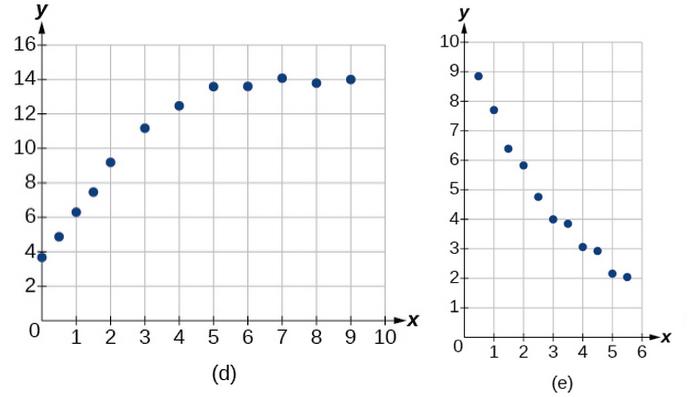6. [latex]y=10.209{e}^{-0.294x}[/latex] 7. [latex]y=5.598 – 1.912mathrm{ln}left(xright)[/latex] 8. [latex]y=2.104{left(1.479right)}^{x}[/latex] 9. [latex]y=4.607+2.733mathrm{ln}left(xright)[/latex] 10. [latex]y=frac{14.005}{1+2.79{e}^{-0.812x}}[/latex] 11. To the nearest whole number, what is the initial value of a population modeled by the logistic equation [latex]Pleft(tright)=frac{175}{1+6.995{e}^{-0.68t}}[/latex]? What is the carrying capacity? 12. Rewrite the exponential model [latex]Aleft(tright)=1550{left(1.085right)}^{x}[/latex] as an equivalent model with base e. Express the exponent to four significant digits. 13. A logarithmic model is given by the equation [latex]hleft(pright)=67.682 – 5.792mathrm{ln}left(pright)[/latex]. To the nearest hundredth, for what value of p does [latex]hleft(pright)=62[/latex]? 14. A logistic model is given by the equation [latex]Pleft(tright)=frac{90}{1+5{e}^{-0.42t}}[/latex]. To the nearest hundredth, for what value of t does [latex]Pleft(tright)=45[/latex]? 15. What is the y-intercept on the graph of the logistic model given in the previous exercise? For the following exercises, use this scenario: The population P of a koi pond over x months is modeled by the function [latex]Pleft(xright)=frac{68}{1+16{e}^{-0.28x}}[/latex]. 16. Graph the population model to show the population over a span of 3 years. 17. What was the initial population of koi? 18. How many months will it take before there are 20 koi in the pond? 19. Use the intersect feature to approximate the number of months it will take before the population of the pond reaches half its carrying capacity. For the following exercises, use this scenario: The population P of an endangered species habitat for wolves is modeled by the function [latex]Pleft(xright)=frac{558}{1+54.8{e}^{-0.462x}}[/latex], where x is given in years. 20. Graph the population model to show the population over a span of 10 years. 21. What was the initial population of wolves transported to the habitat? 22. How many wolves will the habitat have after 3 years? 23. How many years will it take before there are 100 wolves in the habitat? 24. Use the intersect feature to approximate the number of years it will take before the population of the habitat reaches half its carrying capacity. For the following exercises, refer to the table below. x f(x) 1 1125 2 1495 3 2310 4 3294 5 4650 6 6361 25. Use a graphing calculator to create a scatter diagram of the data. 26. Use the regression feature to find an exponential function that best fits the data in the table. 27. Write the exponential function as an exponential equation with base e. 28. Graph the exponential equation on the scatter diagram. 29. Use the intersect feature to find the value of x for which [latex]fleft(xright)=4000[/latex]. For the following exercises, refer to the table below. x f(x) 1 555 2 383 3 307 4 210 5 158 6 122 30. Use a graphing calculator to create a scatter diagram of the data. 31. Use the regression feature to find an exponential function that best fits the data in the table. 32. Write the exponential function as an exponential equation with base e. 33. Graph the exponential equation on the scatter diagram. 34. Use the intersect feature to find the value of x for which [latex]fleft(xright)=250[/latex]. For the following exercises, refer to the table below. x f(x) 1 5.1 2 6.3 3 7.3 4 7.7 5 8.1 6 8.6 35. Use a graphing calculator to create a scatter diagram of the data. 36. Use the LOGarithm option of the REGression feature to find a logarithmic function of the form [latex]y=a+bmathrm{ln}left(xright)[/latex] that best fits the data in the table. 37. Use the logarithmic function to find the value of the function when x = 10. 38. Graph the logarithmic equation on the scatter diagram. 39. Use the intersect feature to find the value of x for which [latex]fleft(xright)=7[/latex].
For the following exercises, refer to the table below.
x f(x) 1 7.5 2 6 3 5.2 4 4.3 5 3.9 6 3.4 7 3.1 8 2.9 40. Use a graphing calculator to create a scatter diagram of the data. 41. Use the LOGarithm option of the REGression feature to find a logarithmic function of the form [latex]y=a+bmathrm{ln}left(xright)[/latex] that best fits the data in the table. 42. Use the logarithmic function to find the value of the function when x = 10. 43. Graph the logarithmic equation on the scatter diagram. 44. Use the intersect feature to find the value of x for which [latex]fleft(xright)=8[/latex].
For the following exercises, refer to the table below.
x f(x) 1 8.7 2 12.3 3 15.4 4 18.5 5 20.7 6 22.5 7 23.3 8 24 9 24.6 10 24.8 45. Use a graphing calculator to create a scatter diagram of the data. 46. Use the LOGISTIC regression option to find a logistic growth model of the form [latex]y=frac{c}{1+a{e}^{-bx}}[/latex] that best fits the data in the table. 47. Graph the logistic equation on the scatter diagram. 48. To the nearest whole number, what is the predicted carrying capacity of the model? 49. Use the intersect feature to find the value of x for which the model reaches half its carrying capacity. For the following exercises, refer to the table below. x f(x) 0 12 2 28.6 4 52.8 5 70.3 7 99.9 8 112.5 10 125.8 11 127.9 15 135.1 17 135.9 50. Use a graphing calculator to create a scatter diagram of the data. 51. Use the LOGISTIC regression option to find a logistic growth model of the form [latex]y=frac{c}{1+a{e}^{-bx}}[/latex] that best fits the data in the table. 52. Graph the logistic equation on the scatter diagram. 53. To the nearest whole number, what is the predicted carrying capacity of the model? 54. Use the intersect feature to find the value of x for which the model reaches half its carrying capacity. 55. Recall that the general form of a logistic equation for a population is given by [latex]Pleft(tright)=frac{c}{1+a{e}^{-bt}}[/latex], such that the initial population at time t = 0 is [latex]Pleft(0right)={P}_{0}[/latex]. Show algebraically that [latex]frac{c-Pleft(tright)}{Pleft(tright)}=frac{c-{P}_{0}}{{P}_{0}}{e}^{-bt}[/latex]. 56. [latex]frac{c-Pleft(tright)}{Pleft(tright)}=frac{c-frac{c}{1+a{e}^{-bt}}}{frac{c}{1+a{e}^{-bt}}}=frac{frac{cleft(1+a{e}^{-bt}right)-c}{1+a{e}^{-bt}}}{frac{c}{1+a{e}^{-bt}}}=frac{frac{cleft(1+a{e}^{-bt}-1right)}{1+a{e}^{-bt}}}{frac{c}{1+a{e}^{-bt}}}=1+a{e}^{-bt}-1=a{e}^{-bt}[/latex] 57. Working with the right side of the equation we show that it can also be rewritten as [latex]a{e}^{-bt}[/latex]. But first note that when t = 0, [latex]{P}_{0}=frac{c}{1+a{e}^{-bleft(0right)}}=frac{c}{1+a}[/latex]. Therefore, 58. Use a graphing utility to find an exponential regression formula [latex]fleft(xright)[/latex] and a logarithmic regression formula [latex]gleft(xright)[/latex] for the points [latex]left(1.5,1.5right)[/latex] and [latex]left(8.5,text{ 8}text{.5}right)[/latex]. Round all numbers to 6 decimal places. Graph the points and both formulas along with the line y = x on the same axis. Make a conjecture about the relationship of the regression formulas. 59. Verify the conjecture made in the previous exercise. Round all numbers to six decimal places when necessary. 60. Find the inverse function [latex]{f}^{-1}left(xright)[/latex] for the logistic function [latex]fleft(xright)=frac{c}{1+a{e}^{-bx}}[/latex]. Show all steps. 61. Use the result from the previous exercise to graph the logistic model [latex]Pleft(tright)=frac{20}{1+4{e}^{-0.5t}}[/latex] along with its inverse on the same axis. What are the intercepts and asymptotes of each function?
Licenses & Attributions
Source: https://t-tees.com
Category: WHICH
