A reciprocal function is more than just the inverse of a given function. It’s the multiplicative inverse and can be found in various types of functions such as trigonometric, logarithmic, and polynomial functions. Let’s dive deeper into the concept of reciprocal functions, their properties, how to graph them, and how to solve them, with plenty of examples and FAQs.
What Are Reciprocal Functions?
Reciprocal functions are obtained by finding the inverse of a given function. For example, if we have a function f(x) = x, its reciprocal function would be f(x) = 1/x. The reciprocal function is also known as the multiplicative inverse.
You are viewing: The Fascinating World of Reciprocal Functions
Exploring the Properties of Reciprocal Functions
Reciprocal functions have some distinct properties. They are typically in the form of a fraction, with a numerator that is a real number and a denominator that can be a number, variable, or polynomial. The reciprocal of x is simply 1/x. Additionally, the domain and range of a reciprocal function are all real numbers except 0, and its graph is symmetric with the equation y = x.
How to Graph Reciprocal Functions
Read more : Which Of The Following Does Not Constitute Spillage
Let’s take a closer look at how to graph a reciprocal function. Consider the function f(x) = 1/x. The graph of this function never touches the x-axis or y-axis. The y-axis acts as a vertical asymptote, as the curve gets very close to it but never intersects. Similarly, the x-axis serves as the horizontal asymptote, as the curve never touches it.
Here’s an illustration to help you visualize it:
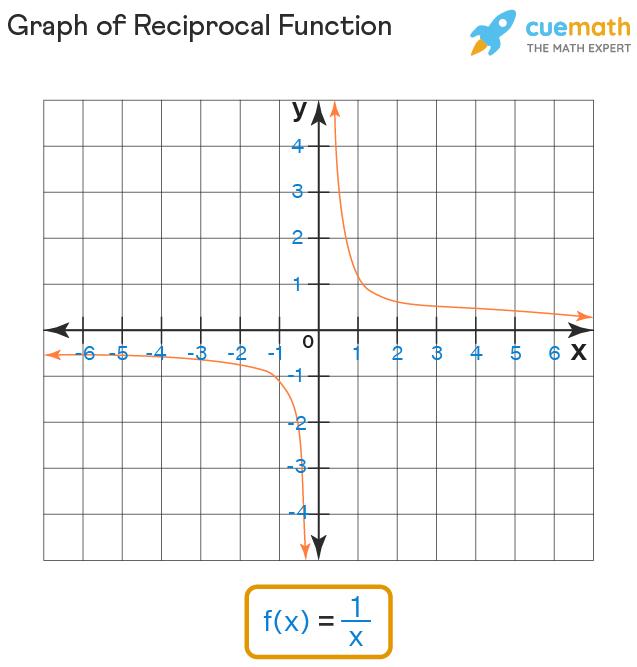
Understanding the Domain and Range
The domain of a reciprocal function is all real numbers except those that result in infinity when divided by 0. In other words, x can be any real number except 0. The range of a reciprocal function is also all real numbers.
To summarize:
- Domain: { x ∈ R: x ≠ 0 }
- Range: { x ∈ R: x ≠ 0 }
Solving Reciprocal Functions
Read more : Which La Crema Chardonnay Is Better
Solving reciprocal functions involves finding their reciprocals using specific methods. Here are some examples:
- Reciprocal of a Number: Divide the number, variable, or expression by 1. For example, the reciprocal of 6 is 1/6.
- Reciprocal of a Variable: Divide the variable by 1. For example, the reciprocal of y is 1/y.
- Reciprocal of an Expression: Exchange the numerator and denominator. For example, the reciprocal of x/(x – 4) is (x – 4)/x.
- Reciprocal of a Fraction: Flip the numerator and denominator. For example, the reciprocal of 5/8 is 8/5.
- Reciprocal of a Mixed Fraction: Convert the mixed fraction to an improper fraction, then find its reciprocal. For example, the reciprocal of 3 3/4 is 4/15 after converting to the improper fraction 15/4.
Important Notes
Here are some key points to remember about reciprocal functions:
- The reciprocal function of f(x) is given by 1/f(x).
- The reciprocal function is often referred to as the multiplicative inverse.
- The domain of the reciprocal function y = 1/x is all real numbers except 0, and the range is also all real numbers except 0.
- Reciprocal functions have a vertical asymptote (y-axis) and a horizontal asymptote (x-axis).
- The vertical asymptote corresponds to the domain, and the horizontal asymptote corresponds to the range of the function.
More Insights
To deepen your understanding of reciprocal functions, you may want to explore related topics such as types of functions, inverse functions, domain and range, graphing functions, and the relationship between functions.
Reciprocal functions offer a fascinating realm to explore in mathematics. Understanding their properties and how to graph and solve them opens up a world of possibilities. So, let’s dive in and discover the endless wonders of reciprocal functions together!
Source: https://t-tees.com
Category: WHICH
