A cubic function is a polynomial function of degree 3. So the graph of a cube function may have a maximum of 3 roots. i.e., it may intersect the x-axis at a maximum of 3 points. Since complex roots always occur in pairs, a cubic function always has either 1 or 3 real zeros. It cannot have 2 real zeros.
Let us learn more about a cubic function along with its domain, range, and the process of graphing it. Let us also learn how to find the critical points and inflection points of a cube function and let us also see its end behavior.
You are viewing: Which Of The Following Graphs Could Represent A Cubic Function
1. What is Cubic Function? 2. Intercepts of a Cubic Function 3. End Behavior of Cube Function 4. Critical and Inflection Points of Cubic Function 5. Cubic Graph 6. FAQs on Cubic Function
A cubic function is a polynomial function of degree 3 and is of the form f(x) = ax3 + bx2 + cx + d, where a, b, c, and d are real numbers and a ≠ 0. The basic cubic function (which is also known as the parent cube function) is f(x) = x3. Since a cubic function involves an odd degree polynomial, it has at least one real root. For example, there is only one real number that satisfies x3 = 0 (which is x = 0) and hence the cubic function f(x) = x3 has only one real root (the other two roots are complex numbers). Here are some examples of a cubic function.
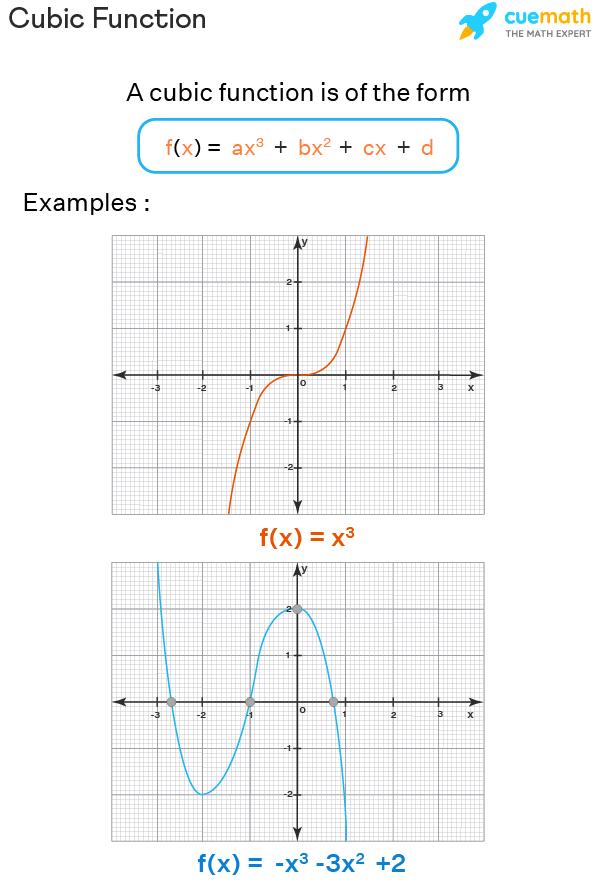
A cubic function is an algebraic function as all algebraic functions are polynomial functions.
Domain and Range of Cubic Function
Since a cubic function y = f(x) is a polynomial function, it is defined for all real values of x and hence its domain is the set of all real numbers (R). Also, if you observe the two examples (in the above figure), all y-values are being covered by the graph, and hence the range of a cubic function is the set of all numbers as well. Thus, we conclude that
- The domain of a cubic function is R.
- The range of a cubic function is R.
Asymptotes of Cube Function
The asymptotes always correspond to the values that are excluded from the domain and range. Since both the domain and range of a cubic function is the set of all real numbers, no values are excluded from either the domain or the range. Hence a cubic function neither has vertical asymptotes nor has horizontal asymptotes.
As we know, there are two types of intercepts of a function: x-intercept(s) and y-intercept(s). Let us see how to find the intercepts of a cubic function.
X-Intercept of Cubic Function
The x-intercepts of a function are also known as roots (or) zeros. As the degree of a cubic function is 3, it can have a maximum of 3 roots. Since complex roots of any function always occur in pairs, a function will always have 0, 2, 4, … complex roots. So a function can either have 0 or two complex roots. Thus, it has one or three real roots or x-intercepts. To find the x-intercept(s) of a cubic function, we just substitute y = 0 (or f(x) = 0) and solve for x-values.
Example: To find the x-intercept(s) of f(x) = x3 – 4×2 + x – 4, substitute f(x) = 0. Then
x3 – 4×2 + x – 4 = 0
x2 (x – 4) + 1 (x – 4) = 0
(x – 4) (x2 + 1) = 0
Read more : Which Pope Changed The 2nd Commandment
x – 4 = 0; x2 + 1 = 0
x = 4 ; x2 = -1
x = 4 ; x = ± i
Complex numbers cannot be the x-intercepts. Therefore, f(x) has only one x-intercept which is (4, 0).
Y-Intercept of Cubic Function
A cubic function always has exactly one y-intercept. To find the y-intercept of a cubic function, we just substitute x = 0 and solve for y-value.
Example: To find the y-intercept of f(x) = x3 – 4×2 + x – 4, substitute x = 0. Then f(x) = 03 – 4(0)2 + (0) – 4 = -4.
Therefore, the y-intercept of the function is (0, -4).
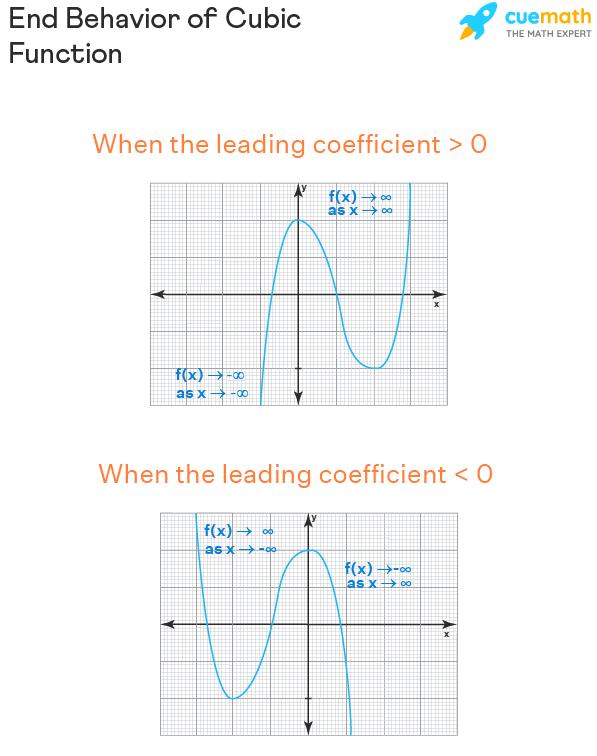
The end behavior of any function depends upon its degree and the sign of the leading coefficient. A cube function f(x) = ax3 + bx2 + cx + d has an odd degree polynomial in it. So its end behavior is as follows:
- When the leading coefficient is positive (a > 0): f(x) → ∞ as x → ∞ and f(x) → -∞ as x → -∞ In this case, the shape of the graph is from bottom to top.
- When the leading coefficient is negative (a < 0): f(x) → -∞ as x → ∞ and f(x) → ∞ as x → -∞ In this case, the shape of the graph is from top to bottom.
We can better understand this from the figure below:
The critical points and inflection points play a crucial role in graphing a cubic function. Let us see how to find them.
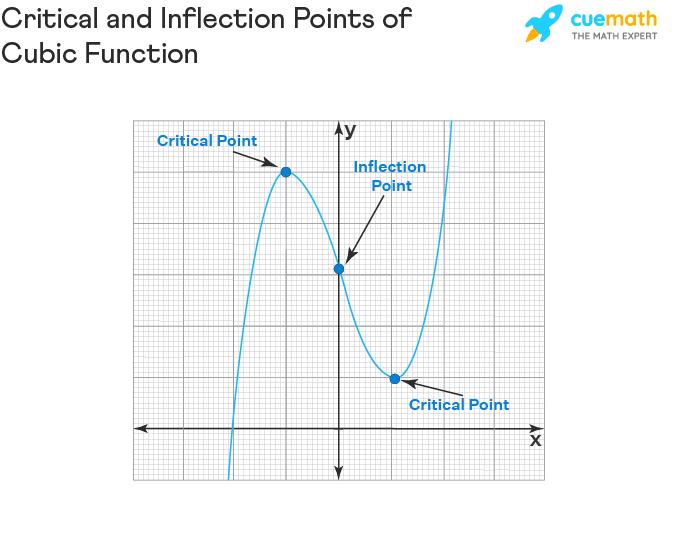
Critical Points of Cubic Function
The critical points of a function are the points where the function changes from either “increasing to decreasing” or “decreasing to increasing”. i.e., a function may have either a maximum or minimum value at the critical point. To find the critical points of a cubic function f(x) = ax3 + bx2 + cx + d, we set the first derivative to zero and solve. i.e.,
f'(x) = 0
3ax2 + 2bx + c = 0
Read more : Which Better Call Saul Character Are You Buzzfeed
This is a quadratic equation and we can solve it using the techniques of solving quadratic equations.
By quadratic formula,
x = (dfrac{-2b pm sqrt{4b^{2}-12 a c}}{6 a}) (or)
x = (dfrac{-b pm sqrt{b^{2}-3 a c}}{3 a})
Hence:
- f(x) has two critical points if b2 – 3ac > 0
- f(x) has only one critical point if b2 – 3ac = 0
- f(x) has no critical point if b2 – 3ac < 0
Inflection Points of Cubic Function
The inflection points of a function are the points where the function changes from either “concave up to concave down” or “concave down to concave up”. To find the critical points of a cubic function f(x) = ax3 + bx2 + cx + d, we set the second derivative to zero and solve. i.e.,
f”(x) = 0
6ax + 2b = 0
6ax = -2b
x = -b/3a
Thus, the cubic function f(x) = ax3 + bx2 + cx + d has inflection point at (-b/3a, f(-b/3a)).
Here are the steps to graph a cubic function. The steps are explained with an example where we are going to graph the cubic function f(x) = x3 – 4×2 + x – 4.
- Step 1: Find the x-intercept(s). We already found that the x-intercept of f(x) = x3 – 4×2 + x – 4 is (4, 0).
- Step 2: Find the y-intercept. We already found that the y-intercept of f(x) = x3 – 4×2 + x – 4 is (0, -4).
- Step 3: Find the critical point(s) by setting f'(x) = 0. 3×2 – 8x + 1 = 0. By quadratic formula, x = (-8 ± √64 – 12) / (6) ≈ 0.131 and 2.535
- Step 4: Find the corresponding y-coordinate(s) of the critical points by substituting each of them in the given function. f(0.131) ≈ -3.935 f(2.535) ≈ -10.879 Therefore, the critical points are (0.131, -3.935) and (2.535, -10.879).
- Step 5: Find the end behavior of the function. Since the leading coefficient of the function is 1 which is > 0, its end behavior is: f(x) → ∞ as x → ∞ and f(x) → -∞ as x → -∞
- Step 6: Plot all the points from Step 1, Step 2, and Step 4. Join them by a curve (also extend the curve on both sides) keeping the end behavior from Step 5 in mind.
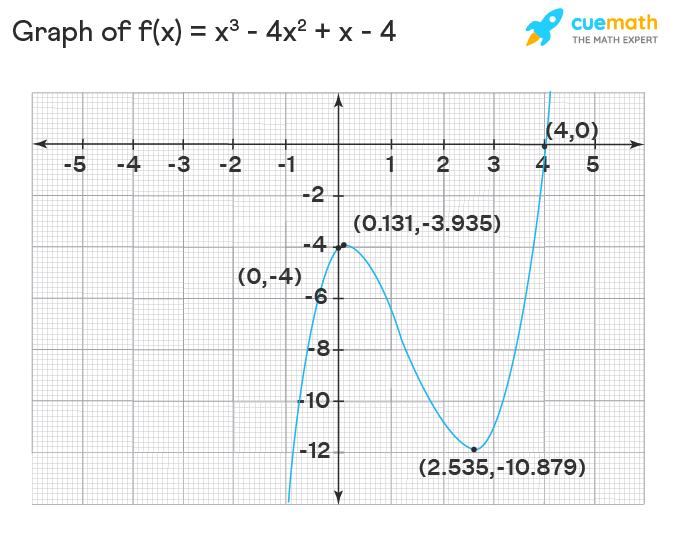
Note: We can compute a table of values by taking some random numbers for x and computing the corresponding y values to know the perfect shape of the graph. Also, we can find the inflection point and cross-check the graph.
Important Notes on Cubic Function:
- A cubic function is of the form f(x) = ax3 + bx2 + cx + d, where a, b, c, and d are constants and a ≠ 0.
- The degree of a cubic function is 3.
- A cubic function may have 1 or 3 real roots.
- A cubic function may have 0 or 2 complex roots.
- A cubic function is maximum or minimum at the critical points.
☛Related Topics:
- Cubic Polynomials
- Cubic Equation Solver
- Graphing Functions
- Graphing Calculator
Source: https://t-tees.com
Category: WHICH
