Literal equations are equations involving letters and alphabets. Equations that consist of variables where each variable signifies a meaning/quantity ‘literally’, they are called literal equations. Some common examples of literal equations are formulas in geometry like the area of a square is given by A = s2, where s denotes the length of a side of the square and A denotes its area.
In this article, we understand the concept of literal equations and how to solve them with the help of some examples and practice questions. A literal equation consists of two or more variables such that one variable can be expressed in terms of other variables.
You are viewing: Which Of These Is An Example Of A Literal Equation
1. What are Literal Equations? 2. Literal Equations Formula 3. Use of Literal Equations 4. Solving Literal Equations 5. FAQs on Literal Equations
Sometimes, we are given equations in the form of formulas of geometric figures, for example, the perimeter of a square is given by P = 4s, where P is the perimeter of the square and s is the side length of the square. We have two variables P. and s such that P is expressed in terms of s. This is an example of a literal equation. In literal equations, we cannot obtain the exact numerical value of a variable.
Literal Equations Definition
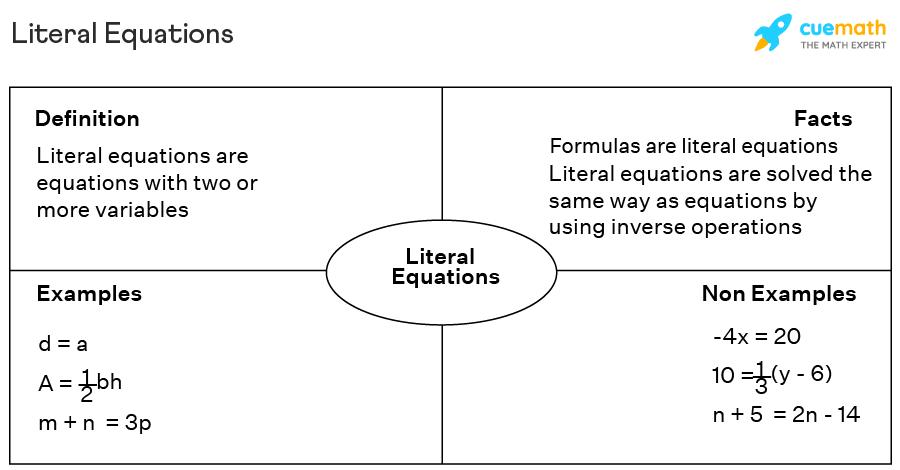
Literal equations are defined as the equations consisting of two or more variables (letters or alphabets) such that each variable can be expressed in terms of other variables. While solving literal equations, the goal is to isolate one variable and express the solution explicitly in terms of the remaining variables. Each variable in a literal equation signifies a quantity.
There is no one fixed formula to solve literal equations. We can identify a literal equation if it has more than one distinct variable. Literal equations can be linear equations, quadratic equations, cubic equations, etc. Literal equations can be solved by expressing each variable of the equation explicitly in terms of other variables. Please note that if the same variable appears in different forms in an equation, the equation may not be a literal equation. Let us consider an example to understand this:
For example: Equation x + x2 + 1 = 0 is not a literal equation because it contains only one variable, that is, x but in different forms. The only variable that appears in this equation is x.
Read more : Which State Has The Most Cockroaches
Literal Equations are commonly used in formulas in mathematics and physics. Some common examples of literal equations are:
- Mass-Energy equation: E = mc2. There are 3 variables in this literal equation, namely E, m, c, and each variable signifies a physical quantity.
- Area of a circle: A = πr2. There are 2 variables in this literal equation, namely A and r, where A is the area and r is the radius.
- Volume of a sphere: V = (4/3)πr3. There are 2 variables in this literal equation, namely A and r, where V is the volume and r is the radius.
- Algebraic equation: x + y = 1. There are 2 variables in this literal equation, namely x and y.
Literal Equations can be solved by isolating one variable and expressing it in terms of other variables. Sometimes, we are given the formula to determine the area of a geometric figure and we need to derive the formula to determine the side length of the figure. Steps to solve literal equations are:
- Identify the variable that you want to have alone.
- Treat all other variables/letters as numbers.
- Add, subtract, or multiply by a variable.
- You can also divide by a variable as long as it is never zero.
- Use all of the rules of algebra that we use to solve algebraic equations.
- Isolate the variable on one side of the equation and hence, obtain the solution
Let us consider a few examples and solve literal equations to understand better.
Example 1: Formula to determine the area of a rectangle is given by, A = lb, where A denotes the area, l denotes the length and b denotes the breadth of the rectangle. We need to derive the formula to determine the length of the rectangle. We have,
A = lb, We need to isolate l and express it in terms of A and b. Divide both sides of the equation by b (as the breadth of a rectangle can never be 0)
A/b = lb/b ⇒ l = A/b
We have solved the literal equation A = lb for l and obtained the formula for l to be l = A/b.
Let us consider another example of an algebraic literal equation and solve it.
Read more : Which Powers Best Complete This Graphic
Example 2: Solve the literal equation 2x + 7y = 12 for x.
We want the variable x to be alone on one side of the equation and y on the other side. Add the negative of 7y to both sides of the equation 2x + 7y = 12.
2x + 7y + (-7y) = 12 + (-7y)
2x = 12 – 7y, Divide all terms of the literal equation by the coefficcient of x to isolate the variable, that is, divide the equation by 2.
2x/2 = (12 – 7y)/2
x = (12 – 7y)/2 = 6 – 7y/2
Hence the solution of the literal equation 2x + 7y = 12 is x = 6 – 7y/2
Important Notes on Literal Equations
- A literal equation is an equation where variables represent known values.
- Literal Equations are used to give formulas like distance, speed, area, volume, force, time, temperature, etc.
- To solve literal equations, isolate the variable and express it as a combination of the remaining variables.
Related Topics on Literal Equations
- Variables, Constants and Expressions
- Variables Expressions
- Linear Equations in Two Variables
Source: https://t-tees.com
Category: WHICH
