The revenue in millions of dollars for a fictional cable company from 2006 through 2013 is shown in the table below.

Year 2006 2007 2008 2009 2010 2011 2012 2013 Revenue 52.4 52.8 51.2 49.5 48.6 48.6 48.7 47.1

You are viewing: Which Polynomial Function Is Graphed Below

The revenue can be modeled by the polynomial function

[latex]Rleft(tright)=-0.037{t}^{4}+1.414{t}^{3}-19.777{t}^{2}+118.696t – 205.332[/latex]

where R represents the revenue in millions of dollars and t represents the year, with t = 6 corresponding to 2006. Over which intervals is the revenue for the company increasing? Over which intervals is the revenue for the company decreasing? These questions, along with many others, can be answered by examining the graph of the polynomial function. We have already explored the local behavior of quadratics, a special case of polynomials. In this section we will explore the local behavior of polynomials in general.

Multiplicity and Turning Points

Graphs behave differently at various x-intercepts. Sometimes the graph will cross over the x-axis at an intercept. Other times the graph will touch the x-axis and bounce off.

Suppose, for example, we graph the function [latex]fleft(xright)=left(x+3right){left(x – 2right)}^{2}{left(x+1right)}^{3}[/latex].

Notice in the figure below that the behavior of the function at each of the x-intercepts is different.

The x-intercept [latex]x=-3[/latex] is the solution to the equation [latex]left(x+3right)=0[/latex]. The graph passes directly through the x-intercept at [latex]x=-3[/latex]. The factor is linear (has a degree of 1), so the behavior near the intercept is like that of a line; it passes directly through the intercept. We call this a single zero because the zero corresponds to a single factor of the function.

The x-intercept [latex]x=2[/latex] is the repeated solution to the equation [latex]{left(x – 2right)}^{2}=0[/latex]. The graph touches the axis at the intercept and changes direction. The factor is quadratic (degree 2), so the behavior near the intercept is like that of a quadratic—it bounces off of the horizontal axis at the intercept.

Read more : Which Statement About Marketing Activities Is Most Accurate

[latex]{left(x – 2right)}^{2}=left(x – 2right)left(x – 2right)[/latex]

The factor is repeated, that is, the factor [latex]left(x – 2right)[/latex] appears twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity. The zero associated with this factor, [latex]x=2[/latex], has multiplicity 2 because the factor [latex]left(x – 2right)[/latex] occurs twice.

The x-intercept [latex]x=-1[/latex] is the repeated solution of factor [latex]{left(x+1right)}^{3}=0[/latex]. The graph passes through the axis at the intercept but flattens out a bit first. This factor is cubic (degree 3), so the behavior near the intercept is like that of a cubic with the same S-shape near the intercept as the function [latex]fleft(xright)={x}^{3}[/latex]. We call this a triple zero, or a zero with multiplicity 3.

For zeros with even multiplicities, the graphs touch or are tangent to the x-axis at these x-values. For zeros with odd multiplicities, the graphs cross or intersect the x-axis at these x-values. See the graphs below for examples of graphs of polynomial functions with multiplicity 1, 2, and 3.

For higher even powers, such as 4, 6, and 8, the graph will still touch and bounce off of the x-axis, but for each increasing even power the graph will appear flatter as it approaches and leaves the x-axis.

For higher odd powers, such as 5, 7, and 9, the graph will still cross through the x-axis, but for each increasing odd power, the graph will appear flatter as it approaches and leaves the x-axis.

Determining End Behavior

As we have already learned, the behavior of a graph of a polynomial function of the form

[latex]fleft(xright)={a}_{n}{x}^{n}+{a}_{n – 1}{x}^{n – 1}+…+{a}_{1}x+{a}_{0}[/latex]

will either ultimately rise or fall as x increases without bound and will either rise or fall as x decreases without bound. This is because for very large inputs, say 100 or 1,000, the leading term dominates the size of the output. The same is true for very small inputs, say -100 or -1,000.

Recall that we call this behavior the end behavior of a function. As we pointed out when discussing quadratic equations, when the leading term of a polynomial function, [latex]{a}_{n}{x}^{n}[/latex], is an even power function, as x increases or decreases without bound, [latex]fleft(xright)[/latex] increases without bound. When the leading term is an odd power function, as x decreases without bound, [latex]fleft(xright)[/latex] also decreases without bound; as x increases without bound, [latex]fleft(xright)[/latex] also increases without bound. If the leading term is negative, it will change the direction of the end behavior. The table below summarizes all four cases.

Even Degree Odd Degree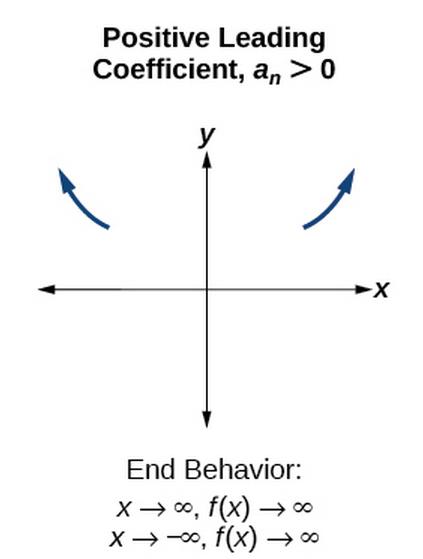

Graphing Polynomial Functions

Read more : Which Is Associated With A Deposition

We can use what we have learned about multiplicities, end behavior, and turning points to sketch graphs of polynomial functions. Let us put this all together and look at the steps required to graph polynomial functions.

The Intermediate Value Theorem

In some situations, we may know two points on a graph but not the zeros. If those two points are on opposite sides of the x-axis, we can confirm that there is a zero between them. Consider a polynomial function f whose graph is smooth and continuous. The Intermediate Value Theorem states that for two numbers a and b in the domain of f, if a < b and [latex]fleft(aright)ne fleft(bright)[/latex], then the function f takes on every value between [latex]fleft(aright)[/latex] and [latex]fleft(bright)[/latex].

We can apply this theorem to a special case that is useful for graphing polynomial functions. If a point on the graph of a continuous function f at [latex]x=a[/latex] lies above the x-axis and another point at [latex]x=b[/latex] lies below the x-axis, there must exist a third point between [latex]x=a[/latex] and [latex]x=b[/latex] where the graph crosses the x-axis. Call this point [latex]left(c,text{ }fleft(cright)right)[/latex]. This means that we are assured there is a value c where [latex]fleft(cright)=0[/latex].

In other words, the Intermediate Value Theorem tells us that when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis. The figure below shows that there is a zero between a and b.

Writing Formulas for Polynomial Functions

Now that we know how to find zeros of polynomial functions, we can use them to write formulas based on graphs. Because a polynomial function written in factored form will have an x-intercept where each factor is equal to zero, we can form a function that will pass through a set of x-intercepts by introducing a corresponding set of factors.

Local and Global Extrema

With quadratics, we were able to algebraically find the maximum or minimum value of the function by finding the vertex. For general polynomials, finding these turning points is not possible without more advanced techniques from calculus. Even then, finding where extrema occur can still be algebraically challenging. For now, we will estimate the locations of turning points using technology to generate a graph.

Each turning point represents a local minimum or maximum. Sometimes, a turning point is the highest or lowest point on the entire graph. In these cases, we say that the turning point is a global maximum or a global minimum. These are also referred to as the absolute maximum and absolute minimum values of the function.

A local maximum or local minimum at x = a (sometimes called the relative maximum or minimum, respectively) is the output at the highest or lowest point on the graph in an open interval around x = a. If a function has a local maximum at a, then [latex]fleft(aright)ge fleft(xright)[/latex] for all x in an open interval around x = a. If a function has a local minimum at a, then [latex]fleft(aright)le fleft(xright)[/latex] for all x in an open interval around x = a.

A global maximum or global minimum is the output at the highest or lowest point of the function. If a function has a global maximum at a, then [latex]fleft(aright)ge fleft(xright)[/latex] for all x. If a function has a global minimum at a, then [latex]fleft(aright)le fleft(xright)[/latex] for all x.

We can see the difference between local and global extrema below.

Key Concepts

• Polynomial functions of degree 2 or more are smooth, continuous functions.
• To find the zeros of a polynomial function, if it can be factored, factor the function and set each factor equal to zero.
• Another way to find the x-intercepts of a polynomial function is to graph the function and identify the points where the graph crosses the x-axis.
• The multiplicity of a zero determines how the graph behaves at the x-intercept.
• The graph of a polynomial will cross the x-axis at a zero with odd multiplicity.
• The graph of a polynomial will touch and bounce off the x-axis at a zero with even multiplicity.
• The end behavior of a polynomial function depends on the leading term.
• The graph of a polynomial function changes direction at its turning points.
• A polynomial function of degree n has at most n – 1 turning points.
• To graph polynomial functions, find the zeros and their multiplicities, determine the end behavior, and ensure that the final graph has at most n – 1 turning points.
• Graphing a polynomial function helps to estimate local and global extremas.
• The Intermediate Value Theorem tells us that if [latex]fleft(aright) text{and} fleft(bright)[/latex] have opposite signs, then there exists at least one value c between a and b for which [latex]fleft(cright)=0[/latex].

Glossary

global maximum highest turning point on a graph; [latex]fleft(aright)[/latex] where [latex]fleft(aright)ge fleft(xright)[/latex] for all x. global minimum lowest turning point on a graph; [latex]fleft(aright)[/latex] where [latex]fleft(aright)le fleft(xright)[/latex] for all x. Intermediate Value Theorem for two numbers a and b in the domain of f, if [latex]a<b[/latex] and [latex]fleft(aright)ne fleft(bright)[/latex], then the function f takes on every value between [latex]fleft(aright)[/latex] and [latex]fleft(bright)[/latex]; specifically, when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis multiplicity the number of times a given factor appears in the factored form of the equation of a polynomial; if a polynomial contains a factor of the form [latex]{left(x-hright)}^{p}[/latex], [latex]x=h[/latex] is a zero of multiplicity p.

Source: https://t-tees.com
Category: WHICH