Now, we will look at how the solutions of an inequality relate to its graph.
Let’s think about the number line in shown previously again. The point [latex]x=3[/latex] separated that number line into two parts. On one side of 3 are all the numbers less than 3. On the other side of 3 all the numbers are greater than 3. See the figure below.
You are viewing: Which Statements Are True About The Linear Inequality Y 3/4x-2
Similarly, the line [latex]y=x+4[/latex] separates the plane into two regions.
On one side of the line are points with [latex]y lt x+4[/latex].
On the other side of the line are the points with [latex]y > x+4[/latex].
We call the line [latex]y=x+4[/latex] a boundary line.
Read more : Which Is Better Moringa Powder Or Capsules
For an inequality in one variable, the endpoint is shown with a parenthesis or a bracket depending on whether or not a is included in the solution:
Similarly, for an inequality in two variables, the boundary line is shown with a solid or dashed line to show whether or not it the line is included in the solution.
[latex]begin{array}{ll} Ax+By lt C & Ax+By leq C Ax+By > C & Ax+By geq C text{Boundary line is }Ax+By=C. & text{Boundary line is }Ax+By=C. text{Boundary line is not included in solution.} & text{Boundary line is included in solution.} text{Boundary line is dashed.} & text{Boundary line is solid.} end{array}[/latex]
Now, let’s take a look at what we found in the figure below. We’ll start by graphing the line [latex]y=x+4[/latex], and then we’ll plot the five points we tested, as shown in the graph.
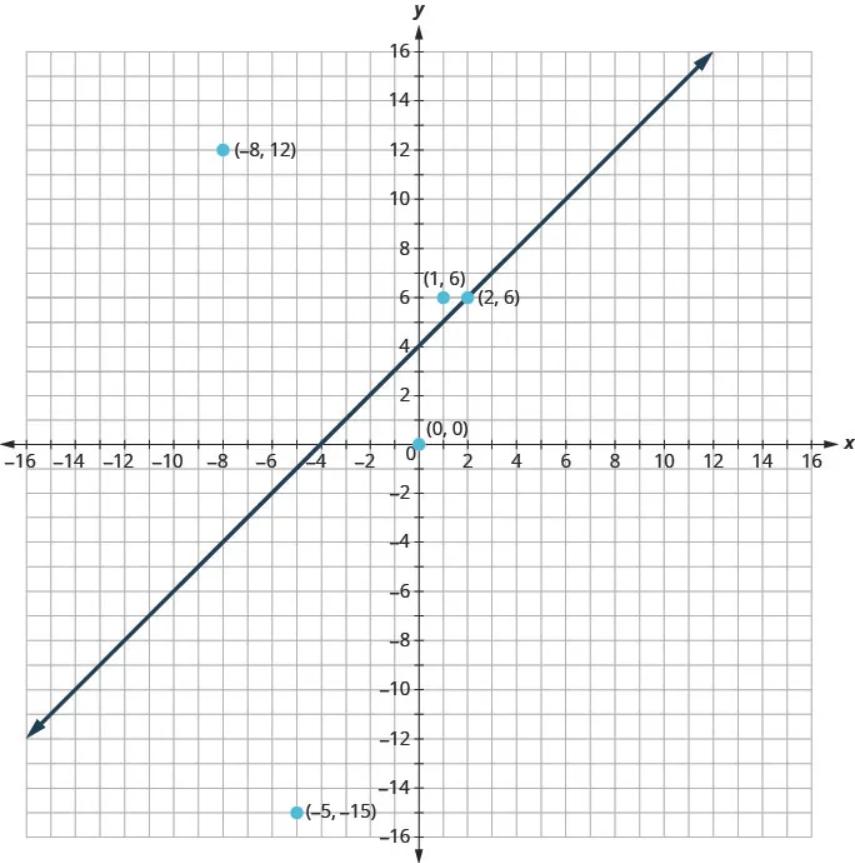
We found that some of the points were solutions to the inequality [latex]y>x+4[/latex] and some were not.
Which of the points we plotted are solutions to the inequality [latex]y>x+4[/latex] ?
The points [latex](1,6)[/latex] and [latex](-8,12)[/latex] are solutions to the inequality [latex]y>x+4[/latex]. Notice that they are both on the same side of the boundary line [latex]y=x+4[/latex].
Read more : Which Is A Valid Proportion
The two points [latex](0,0)[/latex] and [latex](-5,-15)[/latex] are on the other side of the boundary line [latex]y=x+4[/latex] and they are not solutions to the inequality [latex]y>x+4[/latex]. For those two points, [latex]y lt x+4[/latex].
What about the point [latex](2,6)[/latex]? Because [latex]6=2+4[/latex] the point is a solution to the equation [latex]y=x+4[/latex], but not a solution to the inequality [latex]y>x+4[/latex]. So the point [latex](2,6)[/latex] is on the boundary line.
Any point you choose above the boundary line is a solution to the inequality [latex]y>x+4[/latex]. All points above the boundary line are solutions.
Similarly, all points below the boundary line, the side with [latex](0,0)[/latex] and [latex](-5,-15)[/latex] are not solutions to [latex]y>x+4[/latex] as shown in the figure.
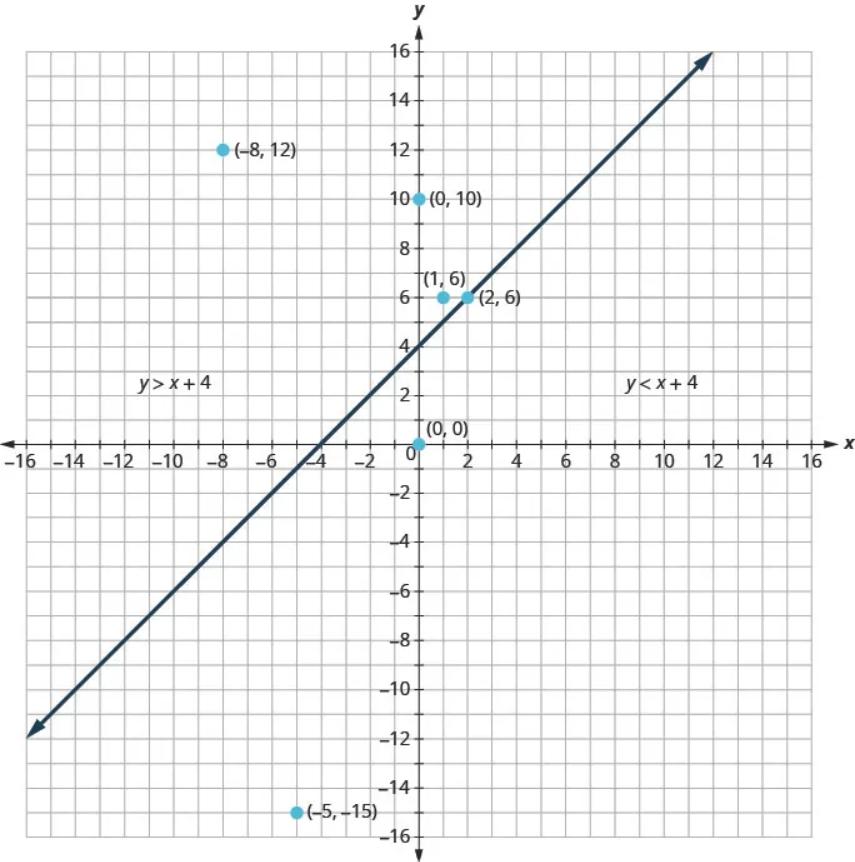
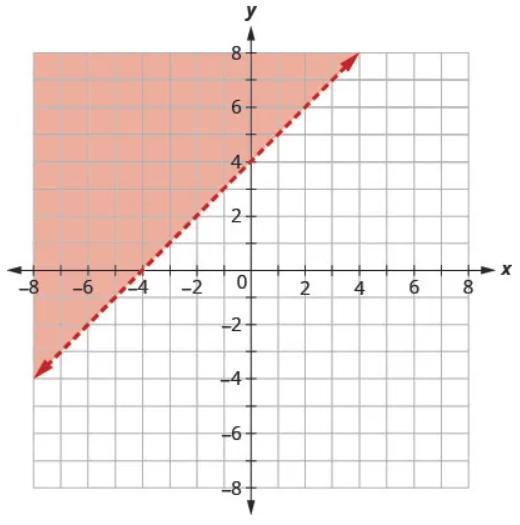
The graph of the inequality [latex]y>x+4[/latex] is shown below.
The line [latex]y=x+4[/latex] divides the plane into two regions. The shaded side shows the solutions to the inequality [latex]y>x+4[/latex].
The points on the boundary line, those where [latex]y=x+4[/latex] are not solutions to the inequality [latex]y>x+4[/latex], so the line itself is not part of the solution. We show that by making the line dashed, not solid.
Source: https://t-tees.com
Category: WHICH
