A tetrahedron is a three-dimensional shape that has four triangular faces. One of the triangles is considered as the base and the other three triangles together form the pyramid. The tetrahedron is a type of pyramid, which is a polyhedron with triangular faces connecting the base to a common point and a flat polygon base. It has a triangular base and thus it is also referred to as a triangular pyramid. Let us learn more about the tetrahedron shape, a regular tetrahedron, tetrahedron angles, and so on in this article.
1. Tetrahedron Definition 2. Net of a Tetrahedron 3. Tetrahedron Properties 4. Surface Area of Tetrahedron 5. Volume of Tetrahedron 6. FAQs on Tetrahedron
You are viewing: Which Types Of Polygons Are The Faces Of A Tetrahedron
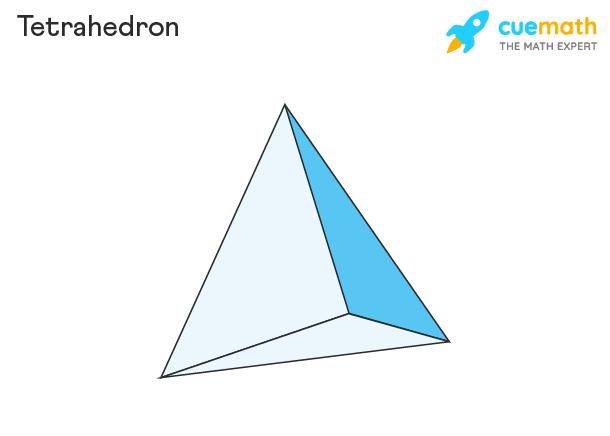
A tetrahedron is also known as a triangular pyramid whose base is also a triangle. A regular tetrahedron has equilateral triangles, therefore, all its interior angles measure 60°. The interior angles of a tetrahedron in each plane add up to 180° as they are triangular. Observe the tetrahedron given below to understand its shape.
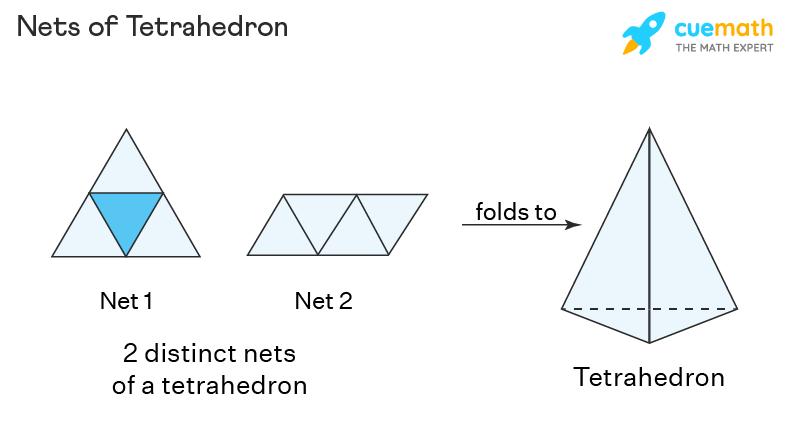
In geometry, a net can be defined as a two-dimensional shape which when folded in a certain manner produces a three-dimensional shape. A tetrahedron is a 3D shape that can be formed using a geometric net. Take a sheet of paper. Observe the two distinct tetrahedron nets shown below. Copy this on the sheet of paper. Cut it along the border and fold it as directed in the figure. The folded paper forms a tetrahedron.
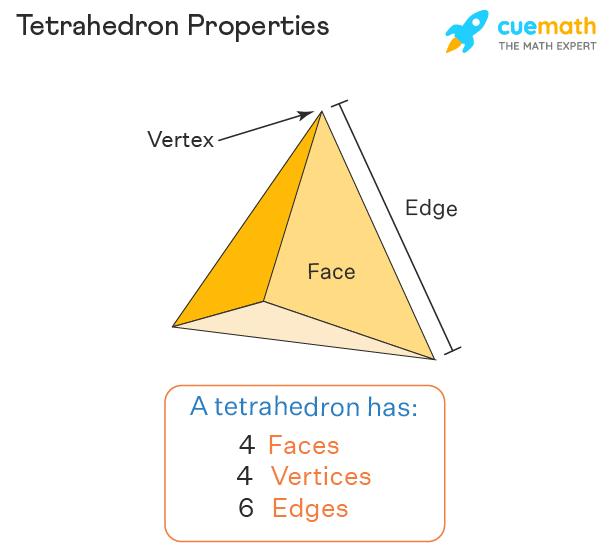
A tetrahedron is a three-dimensional shape that is characterized by some distinct properties. The figure given below shows the faces, edges, and vertices of a tetrahedron.
Tetrahedron Faces Edges Vertices
A tetrahedron is a polyhedron with 4 faces, 6 edges, and 4 vertices, in which all the faces are triangles. Observe the tetrahedron given below to see its faces, vertices, and edges.
The following are the properties of a tetrahedron which help us identify the shape easily.
- It has 4 faces, 6 edges, and 4 vertices (corners).
- In a regular tetrahedron, all four vertices are equidistant from each other.
- It has 6 planes of symmetry.
- Unlike other platonic solids, it has no parallel faces.
- A regular tetrahedron has four equilateral triangles as its faces.
The surface area of a tetrahedron is defined as the total area or region covered by all the faces of the shape. It is expressed in square units, like m2, cm2, in2, ft2, yd2, etc. A tetrahedron can have two types of surface areas:
- Lateral Surface Area of Tetrahedron
- Total Surface Area of Tetrahedron
Lateral Surface Area of a Tetrahedron
Read more : Which Statements Regarding The Involution Process Are Correct
The lateral surface area of a tetrahedron is defined as the surface area of the lateral or the slant faces of a tetrahedron. The formula to calculate the lateral surface area of a regular tetrahedron is given as, LSA of Regular Tetrahedron = Sum of 3 congruent equilateral triangles, i.e., lateral faces = 3 × (√3)/4 a2 where ‘a’ is the side length of a regular tetrahedron.
Total Surface Area of a Tetrahedron
The total surface area of a tetrahedron is defined as the surface area of all the faces of a tetrahedron. The formula to calculate the total surface area of a regular tetrahedron is given as, TSA of Regular Tetrahedron = Sum of 4 congruent equilateral triangles, i.e., all its faces = 4 × (√3)/4 a2 = √3 a2 where ‘a’ is the side length of the regular tetrahedron.
The volume of a tetrahedron is defined as the total space occupied by it in a three-dimensional plane. The formula to calculate the tetrahedron volume is given as, The volume of regular tetrahedron = (1/3) × area of the base × height = (1/3) × (√3)/4 × a2 × (√2)/(√3) a = (√2/12) a3 where ‘a’ is the side length of the regular tetrahedron. The volume of a tetrahedron is expressed in cubic units.
Tetrahedron Angles
In a regular tetrahedron, all the faces are equilateral triangles. Therefore, all the interior angles of a tetrahedron are 60° each. The sum of the face angles for 3 faces of a tetrahedron, that meet at any vertex is 180°.
Important Notes on Tetrahedron
- The 5 platonic solids can be listed as tetrahedron, cube, octahedron, icosahedron, and dodecahedron.
- A tetrahedron is a triangular pyramid with all 4 faces as triangles.
- A tetrahedron has 4 faces, 6 edges, and 4 corners.
☛ Related Topics
- Polyhedron
- Platonic Solids
- Shapes
- Solid Shapes
- 3D Shapes
Source: https://t-tees.com
Category: WHICH
