Because when Pauling defined his electronegativity scale, he had never witnessed #”Kr”#, #”Xe”#, or #”Rn”# making compounds before.
If you want to see the history behind this, and the derivation of the equations he used, scroll down to the very bottom of the answer.
You are viewing: Why Do Noble Gases Have No Electronegativity
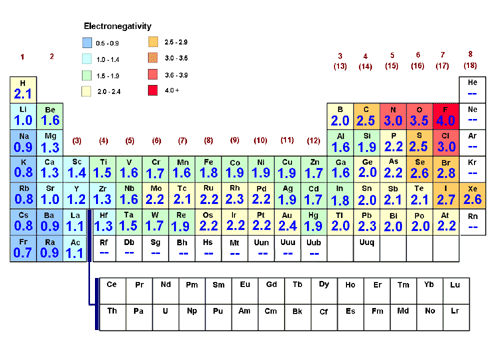
Linus Pauling defined his electronegativity scale (which most general chemistry classes will use) in a way that required knowing experimental bond enthalpies of actual compounds.
He specified that fluorine’s electronegativity was arbitrarily #4.0#, and calculated the remaining electronegativities based on fluorine.
These calculations specifically required that to know the electronegativity of element #”B”#, he must know:
- The electronegativity of element #”A”#
- The bond enthalpy of an #”B”-“B”# bond
- The bond enthalpy of an #”A”-“A”# bond
- The bond enthalpy of an #”A”-“B”# bond
At the time, he had not witnessed #”Kr”#, #”Xe”#, or #”Rn”# making compounds (e.g. #”KrF”_6#, #”XeF”_6#, or #”RnF”_2#), either with themselves or with something else, so he couldn’t assess their electronegativity values.
For all noble gases at the time, Pauling couldn’t have known:
- The bond enthalpy of an #”A”-“B”# bond
- The bond enthalpy of an #”B”-“B”# bond
Thus, he couldn’t find values for them.
So really, it’s more accurate to say that the noble gases, under the Pauling definition of electronegativity, mostly have undefined electronegativity values.
NOTE: However…
Apparently, there is a #”Kr”-“Kr”# (and #”Kr”-“F”#) bond enthalpy: http://www.iem.ac.ru/web-elements-I/Kr.html
Based on that, #”Kr”# should have an electronegativity, and it does. Actually, it’s been determined to be #3.0#.
NOTE: Also…
Apparently, #”Xe”# has an existent electronegativity of #2.6#, because:
- The #”Xe”_2# dimer has been made before.
- Like I said, #”XeF”_6# exists (as well as #”XeF”_2# and #”XeF”_4#).
So, it was possible to find that electronegativity as well.
Read more : Why Is My Wifi Router Blinking Red
NOTE: Oh yes, and…
And you know what, #”Rn”# has an electronegativity too… of #2.2#. I’ve never heard of a radon dimer though, so maybe this is based on accurate theoretical chemistry.
#”RnF”_2# has been made before, though only for a short period of time.
APPENDIX BELOW!
DISCLAIMER: You do not need to know how to calculate the electronegativities of atoms, because Linus Pauling already did. You should just know how to use electronegativities.
Here’s how Linus Pauling came up with the electronegativities in 1932. Coming from a Physical Chemistry background, I have a pretty good understanding of what’s being discussed here.
I will list the equation near the bottom, just so you can know that there was indeed an equation. But you don’t have to know how to use it.
REPRESENTING A MOLECULE
Pauling starts from the wave function (a physical chemistry concept), which, in this particular scenario, describes the interaction of two atoms to make a molecule from the standpoint of quantum mechanics.
He begins with a linear combination of averaged states:
#Psi_(AB) = c_1phi_(AB) + c_2phi_(A^(+)B^(-)) + c_3phi_(B^(+)A^(-))#
where:
- #Psi# is a time-dependent wave function, which basically represents a molecule in this case.
- #phi# is a “trial function“, which just means it’s a function Pauling got from trial and error and used to solve the wave function. In other words, it’s a function he figured out after fidgeting a lot with numbers.
- #c_1#, #c_2#, and #c_3# are expansion coefficients, correlating with the linear combination of atomic orbitals (LCAO) concept. They are a direct experimental result of this linear combination, and they aren’t important to us, specifically.
IONIC/COVALENT CONTRIBUTIONS TO THE CHEMICAL BOND
#A# is bonding member #1# and #B# is bonding member #2#. If it is #(+)#, it is a cation, and if it is #(-)#, it is an anion.
Thus, the functions after the equal sign, in order from left to right, represent the covalent character #”*”#, and then the ionic character #”*”# (where #A# is a cation, and then alternatively, where #B# is a cation).
#”*”# Covalent character: the component that describes a pure covalent bond.
#”*”# Ionic character: each of the two components denotes how it might theoretically be if all electrons belonged to only one of the two contributors in the bond (#A# or #B# only).
The idea with these components is that they basically account for the fact that not all bonds are #100%# “covalent” or #100%# “ionic”.
Read more : Why Is My Car Ac Blowing Warm Air
In other words, if for example, #A# was #”Na”^(+)# and #B# was #”Cl”^(-)#, then you could also say that #A# was #”Na”^(-)# if #B# was #”Cl”^(+)#. That is the ionic character component. Then, you could also have the covalent character component, which means #”Na”-“Cl”#, or perfectly shared electrons: half and half.
This corresponds with the idea of electronegativity, since it implies the potential for unequal sharing of electrons towards the more electronegative atom, which correlates with what we today say electronegativity differences explain.
DEVIATION FROM PERFECTLY EQUAL ELECTRON SHARING
When Pauling proceeds to determine a relationship for calculating electronegativity, he starts with this equation:
#Delta’ = D_(AB) – sqrt(D_(A A) D_(BB))#
where:
- #Delta’# is the “additional ionic character”, which describes the degree/amount/extent of polarization of charge towards one member of the bond or the other.
- #D# is the experimentally-measured bond energy.
- #AB# is a label for two different bonding members. Thus, it stands for the hypothetical interaction of THE two investigated bonding members whose electronegativity differences are unknown.
- #A A# is a label for two identical #A# bonding members, and #BB# for two identical #B# bonding members. Thus, it stands for the hypothetical interactions of two bonding members whose electronegativity differences are #0#.
Hence, that basically says that the amount of polarization towards one bonding member versus the other is somehow dependent on the difference in energy between bonding the two different atoms and bonding two identical atoms.
THESE DEVIATIONS CORRELATE WITH OUR CONCEPT OF ELECTRONEGATIVITY DIFFERENCES
Pauling then postulates that this additional ionic character #Delta’# has something to do with so-called electronegativity differences between the two atoms, and poses the following equation:
#Delta’ = f(“EN”_A – “EN”_B)#
And after fudging with some numbers, he determines that the function is:
#Delta’ = 30(“EN”_A – “EN”_B)#
OVERALL ELECTRONEGATIVITY EQUATION
Thus, the equation he figures out is:
#color(blue)(D_(AB) = sqrt(D_(A A) D_(BB)) + 30(“EN”_A – “EN”_B))#
Overall, what Pauling had to know were the #D# terms-the bond energies for the homonuclear bonding and for the heteronuclear bonding-and the electronegativities #”EN”# of the two bonding members. (Those bonding energies were experimentally-determined.)
Then, since Pauling didn’t know the electronegativities yet, he assigned #4.0# to fluorine and used that to calculate the electronegativities of all the other atoms on the periodic table. Smart, eh?
Source: https://t-tees.com
Category: WHY
